Property c) In terms of height functions, this condition says that there is a unit vector V near N(P) such that _V has two distinct critical points Q₁ and Q₂ near P with _V(Q₁) =  _V(Q₂). For a function graph X(x, y) = (x, y, f(x, y)), this condition translates to N(Q₁) =  (a, b) = N(Q₂) and _{(a,  b)}(Q₁) =  _{(a,  b)}(Q₂), i.e.

f_x(x₁, y₁) =a = f_x(x₂, y₂)
f_y(x₁, y₁) = b = f_y(x₂, y₂)
f(x₁, y₁) + ax₁ + by₁ = f(x₂, y₂) + ax₂ + by₂

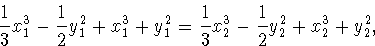
For Menn's surface we use the symmetry about the plane of the second two coordinates. If x₁ = -x₂ and y₁ = y₂, then f(x₁, y₁) = f(x₂, y₂), f_x(x₁, y₁) = -f_x(x₂, y₂), and f_y(x₁, y₁) = f_y(x₂, y₂) Thus if f_x(x, y) = 0, x  0, then Q₁ = (x, y) and Q₂ = (-x, y) will be a pair of distinct points with the same tangent plane. Now 0 = f_x(x, y) = 4x³ + 2xy = 2x(2x² + y) if and only if x = 0 or y = -2x². Since this last curve contains P = (0, 0), (c) holds for Menn's surface. (Note that if  = -1/4, this curve coincides with the parabolic curve, since the Gaussian image of the parabolic curve is a single point. The same thing happens at the top of a torus of revolution.) Theorem 3.1 (c) will be proved in chapter 5.

Property d) Suppose that P in U is not an umbilic point of X, i.e. X has two distinct principal curvatures k₁ and k₂ at P. Let V₁ and V₂ be unit vectors in the corresponding principal directions. Then P is a ridge point of X , with associated principal curvature k₁, if the directional derivative of k₁ in the direction V₁ is zero at P [Por1].

Suppose that the plane g in R³ is a plane of symmetry of the surface X . The intersection of g with the image of X is a ridge curve of X. More precisely if X(P) is in g, then P is either a ridge point or an umbilic point. For let : (-a, a) -> U be a curve with (0) = P, and let  = X ° . If we choose so that r((t)) = (-t), where r is reflection in g, and t is in (-a, a), then '(0) will be in a principal direction. ('(0) is an eigenvector of the Jacobian of the Gauss map of X, by symmetry.) Suppose that P is not an umbilic point, and let k be the principal curvature in the direction of '(0). Along the curve , we have K(t) = K(-t), so K'(0) = 0, i.e. the directional derivative of k in the direction of '(0) is zero, so P is a ridge point of X. Note that for condition (d) to be satisfied, we must also have that K(0) = 0.

The shoe surface has the plane y = 0 as a plane of symmetry, so (t, 0) is a curve of ridge points of X. The parabolic curve is (0, t), so this ridge crosses the parabolic curve at P = (0, 0). We can take (t) = (0, t), the parabolic curve, so (t) = (0, t, -1/2t²), and K(0) is the curvature of at zero, since the plane of is normal to X at P. So K(0)  0, and (d) does not hold at P.

Similarly, the plane x = 0 is a plane of symmetry of Menn's surface, so (0, t) is a ridge curve, which crosses the parabolic curve (t,-(6  + 1)t²) at P = (0, 0). If we let (t) = (t, 0), then (t) = (t, 0, t⁴) and (0) = 0, so (d) does hold at P.

The perturbed monkey saddle has three planes of symmetry: y = 0, y = 3^1/2 x, y = -3^1/2 x. So we have three ridge curves (t, 0), (t,3^1/2 t), (t, -3^1/2 t). Recall that if   0 the parabolic curve is the circle x² + y² =  ², which crosses the ridge curves at the six points r = ||,  = 0, /3, 2/3, , 4/3, 5/3 in polar coordinates. For example consider the ridge curve (t, 0) which crosses the parabolic curve at P₁ = (, 0) and P₂ = (- , 0). Let ₁(t) = ( , t), so ₁(t) = ( , t,4 ³/3). The curvature of ₁ is zero at t = 0 (₁ is a straight line) so (d) is satisfied at P₁. Let ₂(t) = (- , t), so ₂(t) = (- , t, 2³/3 + 2t²), and the curvature of ₂ is zero at t = 0, so (d) is not satisfied at P₂. Since X has 3-fold symmetry about the z-axis, we conclude that if  > 0 then (d) is satisfied at r = ,  = 0, 2/3, 4/3, and if  < 0 then (d) is satisfied at r = -,  = /3, , 5/3.

For surfaces of revolution every plane containing the z-axis is a plane of symmetry, so all the meridians are ridges. Along a circle of latitude corresponding to an inflection of the profile curve, the principal curvature associated to the meridian ridges is constant, nonzero. Along a latitude corresponding to an extremum of the profile curve the principal curvature associated to the meridian ridges is identically zero.

Finally, the warped torus has n vertical planes of symmetry, each of which intersects the parabolic curve in four points, and (d) holds at each of these points.

Theorem 3.1(d) will be proved in chapter 6.

Property e) For example, the parallel surface of a canal surface of a space curve is a parallel tube of . A parallel tube of radius D has swallowtail singularities at those points in space where the osculating sphere of has radius D. (Cf. chapter 6 below.) Thus (e) says that the osculating sphere of has infinite radius, which occurs at the torsion zeros of . Theorem 3.1(e) will be proved in chapter 6.

Property f) If we assume that the singular locus of the pedal surface of X from the point A is a cuspidal edge with isolated swallowtail points, and a degenerate singularity at A itself, then it is easy to check that the swallowtail points of the pedal surface correspond to the cusps of the Gauss map. (This assumption is valid if the Gauss map is stable, as we shall show in chapter 6). For simplicity we assume that A is the origin of R³. The pedal map W of X from the origin is defined by

W = (X ^. N)N,

W_x = (X_x ^. N + X ^. N_x)N + (X ^. N)N_x,

W_y = (X_y ^. N + X ^. N_y)N + (X ^. N)N_y,

W_x x W_y  =  (X_x ^. N + X ^. N_x) (X ^. N) N x N_y
 +  (X_y ^. N + X ^. N_y) (X ^. N) N_x x N
 +  (X ^. N)² N_x x N_y

W(t) = (X(t) ^. N(t))N(t),

W'(t) = (X'(t) ^. N(t) +  X(t) ^. N'(t))N(t) +  (X(t) ^. N(t))N'(t)

If X(t) ^. N(t)  0, then W'(t) = 0 only if N'(t) is parallel to N(t), which can happen only if N'(t) = 0. Thus the cusps of the cuspidal edge W(t), which are the swallowtail points of W, correspond to the cusps of the parabolic image N(t), which are the cusps of the Gauss mapping N.

Theorem 3.1(f) will be proved in chapter 6.

Property g) The space curve (t) has n^th order contact with the surface G(x, y, z) = 0 at the point (t₀) if and only if the function G(t) = G((t)) vanishes to order n at t₀:

The origin (0, 0, 0) is a parabolic point, and the tangent plane at the origin is horizontal. For the tangent line (t) = (t cos s, t sin s, 0), 0 < s < , G⁽²⁾(0) = -sin² s, G⁽³⁾(0) = 2cos³ s, G⁽⁴⁾(0) = 0, so has first order contact with the shoe if s  0 and second order contact if s = 0. Next consider Menn's surface

The perturbed monkey saddle contains the three lines

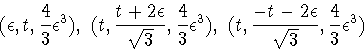
Theorem 3.1(g) will be proved in chapter 7.