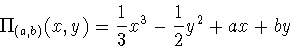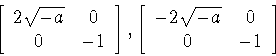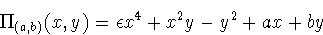Previous: Chapter 2: Examples 4 and 5
Up: Table of Contents
Next: Chapter 3: Characterizations of Gaussian Cusps, Part 2
Chapter 3
Characterizations of Gaussian cusps
The following three theorems will be illustrated in this section by
the five examples of section two.
Theorem 3.1 Let U be an open set in the plane and let
X : U-> R3 be a smooth
immersion. If P in U is a cusp of the Gauss map of
X, then the following statements (a)-(h) are true. Conversely,
if the Gauss map of X is stable, and any of the following
conditions holds, then P is a cusp of the Gauss mapping.
- a)
-
A zero principal curvature direction of X is tangent to the
parabolic curve of X at P.
- b)
-
For each
 > 0 there exist three
distinct points Q1, Q2,
Q3 in U such that
|P - Qi| <
> 0 there exist three
distinct points Q1, Q2,
Q3 in U such that
|P - Qi| <  for i = 1, 2, 3, and the
tangent planes to X at Q1,
Q2, Q3 are parallel.
for i = 1, 2, 3, and the
tangent planes to X at Q1,
Q2, Q3 are parallel.
- c)
-
For each
 > 0 there exist two
distinct points Q1, Q2 in U
such that |P -Qi| <
> 0 there exist two
distinct points Q1, Q2 in U
such that |P -Qi| <  for i = 1, 2, and the tangent
planes to X at Q1 and Q2
are equal.
for i = 1, 2, and the tangent
planes to X at Q1 and Q2
are equal.
- d)
-
P is a ridge point of X as well as a parabolic point of
X , and the principal curvature associated with the ridge is
zero at P.
- e)
-
Given
 > 0 and
d > 0, there exists a point Q in U and
a D > d such that
|P - Q| <
> 0 and
d > 0, there exists a point Q in U and
a D > d such that
|P - Q| <  and
Q is a swallowtail point of the parallel surface to X at
distance D .
and
Q is a swallowtail point of the parallel surface to X at
distance D .
- f)
-
For any point A in R3 which is not on the
tangent plane to X at P, the point P is a
swallowtail point of the pedal surface of X from A.
- g)
-
P is a parabolic point of X , and a line in
R3 has order of contact greater than two with
X at P.
- h)
-
P is a parabolic point of X , and given
 > 0 there exists Q in U
such that |P - Q| <
> 0 there exists Q in U
such that |P - Q| <
 and Q is an inflection point of an
asymptotic curve of X.
and Q is an inflection point of an
asymptotic curve of X.
Our final two characterizations of Gaussian cusps involve notions
which aren't defined for an arbitrary immersion.
Theorem 3.2 Let
X : U->R3 be a smooth
immersion of the planar open set U , and let P be a
parabolic point of X . If P is a cusp of the Gauss map,
and the image of the parabolic curve under X has nonzero
curvature at P , then
- i)
-
The osculating plane at P of the parabolic image curve of
X is the tangent plane of X at P.
Conversely, if the Gauss map is stable, and the parabolic image curve
has nonzero curvature at P , and (i) holds, then P is a
cusp of the Gauss map. Furthermore, the set of immersions such that
the Gauss map is stable and the parabolic image curve has nonzero
curvature at each Gaussian cusp is open and dense in the space of all
immersions of U in R3.
Theorem 3.2, except for the last statement, is due to Bleeker and
Wilson [BlW].
Theorem 3.3 Let
X : U->R3 be a smooth
immersion of the planar open set U , and let P be a
parabolic point of X . If P is a cusp of the Gauss map,
and the asymptotic direction map along the parabolic curve is regular
at P , then
- j)
-
P is an inflection point of the asymptotic direction map of
X.
Conversely, if the Gauss map is stable, and the asymptotic
direction map is regular at P , and (j) holds, then P is a cusp
of the Gauss map. Furthermore, the set of immersions such that the
Gauss map is stable and the asymptotic direction map is regular at
each Gaussian cusp is open and dense in the space of all immersions of
U in R3.
The topology on the space of smooth immersions of U in
R3 is the Whitney C-infinity topology [GolG, p. 42].
Conditions (b), (c), and (i) are related to the contact of the
immersion X with planes in R3 , or to
singularities of projections to lines in R3
. Conditions (d), (e), and (f) reflect the contact of X with
spheres in R3 , or singularities of the
distance-squared function from points of R3
. Conditions (g), (h), and (j) are related to the contact of X
with lines in R3 , or to singularities of
projections of X to planes in R3.
The proofs of these theorems, in chapters 5, 6, and 7, will
actually establish global versions, for immersions in
R3 of any smooth surface.
We now discuss the ten properties (a)-(j), using the five examples
of chapter two.
If P is a cusp of the Gauss map N of X then
there are coordinate charts about P in U and about
N(P) in S2 such that in these
coordinates N takes (x, y) to
(x, y3 - xy). The
curve x = 3y2 of singular
points of N is the parabolic curve of X near
P = (0, 0). Its image by N is the
cuspidal cubic
4u3 = 27v2. If
4u3 > 27v2 there are
exactly three points Q1, Q2,
Q3 such that
N(Qi) = (u, v), and
exactly two of these points
Qi = (xi, yi)
satisfy
xi < 3yi2. If
4u3 < 27v2
there is exactly one point Q = (x, y)
such that N(Q) = (u, v); this
point has x < 3y2. So there are
two distinct types of Gaussian cusps:
- (i)
-
Elliptic cusp. If
x < 3y2 then
(x, y) is elliptic
(K(x, y) > 0), and if
x > 3y2 then
(x, y) is hyperbolic
(K(x, y) < 0).
- (ii)
-
Hyperbolic cusp. If
x < 3y2 then
(x, y) is hyperbolic, and if
x > 3y2 then
(x, y) is elliptic.
If P is a cusp of the Gauss map N of X , then
P is elliptic [hyperbolic] if and only if there exist distinct
elliptic [hyperbolic] points Q1 and
Q2 arbitrarily close to P such that
N(Q1) = N(Q2).
Menn's surface (example 2) has an elliptic Gaussian cusp if
 < -1/4 , and a hyperbolic Gaussian cusp
if
< -1/4 , and a hyperbolic Gaussian cusp
if  > -1/4.
> -1/4.
Property a) If the Gauss mapping is good then its Jacobian
has rank one at each parabolic point P . The kernel of the
Jacobian map is the zero principal curvature direction at
P. Consider a curve
(x(t), y(t)) in the parameter domain
U with Gaussian image N(t). Let
P = (x(0), y(0)) and
V = (x'(0), y'(0)). The curvature of
X in the direction V at P is zero if and only if
N'(0) = 0. If
(x(t), y(t)) is the parabolic curve of
X, and N is excellent, then N'(0) = 0
if and only if P is a cusp of N. This implies theorem
3.1 (a).
The modified Gauss mapping of the shoe surface (example 1) has
Jacobian matrix

so the zero principal curvature direction along the parabolic curve
(0, t) is spanned by the constant vector (1, 0), and
(a) holds for no parabolic point.
The modified Jacobian matrix of Menn's surface is
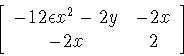
so the zero principal curvature direction along the parabolic
curve (t, -(1 + 6
 )t2) is spanned by the vector
(1, t). If
)t2) is spanned by the vector
(1, t). If 
 -1/4,
this vector is tangent to the parabolic curve if and only if
t = 0, where the Gauss map has a cusp. If
-1/4,
this vector is tangent to the parabolic curve if and only if
t = 0, where the Gauss map has a cusp. If
 = -1/4, the vector (1, t) is
tangent along the entire parabolic curve, and the Gauss map is not
excellent.
= -1/4, the vector (1, t) is
tangent along the entire parabolic curve, and the Gauss map is not
excellent.
The two types of Gaussian cusps can be distinguished from the
viewpoint of (a) as follows. If P is a cusp of the Gauss map of
X, let l be the line of curvature of X which is
tangent to the parabolic curve at P . If P is elliptic
[hyperbolic], then l - {P} is contained in the elliptic
[hyperbolic] region of U (cf. [BlW, p. 287]).
Property b) A plane M is tangent to the surface
X : U->R3 at Q in
U if and only if Q is a critical point of the
composition of X with orthogonal projection to the line
l through the origin normal to M. Then the line
l contains the Gaussian spherical image N(Q).
For a unit vector V in R3 , let
 V : U->R be
the composition of X with the orthogonal projection to the line
spanned by V:
V : U->R be
the composition of X with the orthogonal projection to the line
spanned by V:
 V(P) = X(P) . V
V(P) = X(P) . V
A restatement of (b) is that the height function  N(P) has a degenerate
critical point at P, which splits up into three distinct
critical points Q1, Q2,
Q3 near P for certain height functions
N(P) has a degenerate
critical point at P, which splits up into three distinct
critical points Q1, Q2,
Q3 near P for certain height functions  V with V arbitrarily near
N(P) . We will show in chapter
5 that these three critical points are nondegenerate if P
is a cusp of the Gauss map N. So (b) is equivalent to the
statement that the critical point P of the height function
V with V arbitrarily near
N(P) . We will show in chapter
5 that these three critical points are nondegenerate if P
is a cusp of the Gauss map N. So (b) is equivalent to the
statement that the critical point P of the height function  N(P) has Milnor
number three (cf. [C2]).
N(P) has Milnor
number three (cf. [C2]).
The two types of Gaussian cusps are distinguished from this
viewpoint by their Morse indices. P is an elliptic [hyperbolic]
cusp of the Gauss map N if and only if P is an extremum
[saddle] of  N(P). P
splits up into three nondegenerate critical points: two maxima (or two
minima) and a saddle [two saddles and a maximum (or minimum)]. Note
that
N(P). P
splits up into three nondegenerate critical points: two maxima (or two
minima) and a saddle [two saddles and a maximum (or minimum)]. Note
that  N(Q)
has a nondegenerate critical point at Q which is an extremum
[saddle] if and only if the Gaussian curvature of X at Q
is positive [negative].
N(Q)
has a nondegenerate critical point at Q which is an extremum
[saddle] if and only if the Gaussian curvature of X at Q
is positive [negative].
Now consider a function graph
X(x, y) = (x, y, f(x, y)),
with P = (0, 0) and
N(P) = (0, 0, 1). Then
 N(P)(x, y) = f(x, y). The
family of height functions
N(P)(x, y) = f(x, y). The
family of height functions
 V : U->R,
V : U->R,
 V(x, y) = X(x, y) . V,
with V = (a, b, c),
a2 + b2 + c2 = 1,
c > 0, is equivalent to the family
V(x, y) = X(x, y) . V,
with V = (a, b, c),
a2 + b2 + c2 = 1,
c > 0, is equivalent to the family
 V with a and b
arbitrary and c = 1. Let
V with a and b
arbitrary and c = 1. Let
 (a, b) =
(a, b) =
 (a, b, 1). Then
(a, b, 1). Then
 V(x, y) = f(x, y) + ax + by,
V(x, y) = f(x, y) + ax + by,
a linear perturbation of f(x, y). And
Q is a critical point of
 (a, b) if and only if
(a, b) = Ñ(Q), where
Ñ is the modified Gauss map of X (defined in chapter
2). The Hessian matrix of second partials of
(a, b) if and only if
(a, b) = Ñ(Q), where
Ñ is the modified Gauss map of X (defined in chapter
2). The Hessian matrix of second partials of
 V equals the Hessian matrix of
f(x, y), which is the negative of the
Jacobian matrix of Ñ. Therefore Q is a degenerate
critical point of
V equals the Hessian matrix of
f(x, y), which is the negative of the
Jacobian matrix of Ñ. Therefore Q is a degenerate
critical point of  (a, b)
if and only if Q is a parabolic point of X.
(a, b)
if and only if Q is a parabolic point of X.
For the shoe surface we have the perturbation
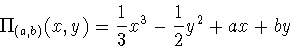
with gradient
(x2 + a, -y + b). If
a > 0,
 (a, b) has no critical points. If
a < 0,
(a, b) has no critical points. If
a < 0,
 (a, b) has critical points
((-a)1/2, b) and
(-(-a)1/2, b) with Hessian matrices
(a, b) has critical points
((-a)1/2, b) and
(-(-a)1/2, b) with Hessian matrices
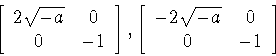
respectively, so ((-a)1/2, b) is a
saddle and (-(-a)1/2, b) is a
maximum. (If a = 0,
 (a, b) has a degenerate critical point at
(0, b).) Therefore f(x, y) has
Milnor number 2 at P = (0, 0). For Menn's surface we
have
(a, b) has a degenerate critical point at
(0, b).) Therefore f(x, y) has
Milnor number 2 at P = (0, 0). For Menn's surface we
have
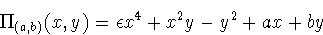
with gradient (4 x3 + 2 xy + a, x2 - 2 y + b). So
(x, y) is a critical point of
x3 + 2 xy + a, x2 - 2 y + b). So
(x, y) is a critical point of
 (a, b) if and only if both
(a, b) if and only if both
- (i)
-
y = -(4
 x3 + a)/2x,
and
x3 + a)/2x,
and
- (ii)
-
(4
 + 1) x3 + bx + a = 0,
+ 1) x3 + bx + a = 0,
provided that x  0. (If x = 0
then a = 0 and y =ف/2b.)
Now if
0. (If x = 0
then a = 0 and y =ف/2b.)
Now if 
 -1/4 then (ii) has
three distinct real roots if and only if its discriminant is negative:
-1/4 then (ii) has
three distinct real roots if and only if its discriminant is negative:

(Note that the locus of zeros of the discriminant is precisely the
image of the parabolic curve of X by the modified Gauss map
Ñ.) If  < -1/4, then
f(x, y) = 0 only if
(x, y) = (0, 0), so f has an
absolute maximum at (0, 0), and
P = (0, 0) is an elliptic Gaussian cusp. If
< -1/4, then
f(x, y) = 0 only if
(x, y) = (0, 0), so f has an
absolute maximum at (0, 0), and
P = (0, 0) is an elliptic Gaussian cusp. If
 > -1/4, then the locus
f(x, y) = 0 is two tangent
parabolas, and f has a topological saddle point at
(0, 0), so P is a hyperbolic Gaussian cusp. Theorem
3.1(b) will be proved in chapter 5.
> -1/4, then the locus
f(x, y) = 0 is two tangent
parabolas, and f has a topological saddle point at
(0, 0), so P is a hyperbolic Gaussian cusp. Theorem
3.1(b) will be proved in chapter 5.
Previous: Chapter 2: Examples 4 and 5
Up: Table of Contents
Next: Chapter 3: Characterizations of Gaussian Cusps, Part 2
 > 0 there exist three
distinct points Q1, Q2,
Q3 in U such that
|P - Qi| <
> 0 there exist three
distinct points Q1, Q2,
Q3 in U such that
|P - Qi| <  for i = 1, 2, 3, and the
tangent planes to X at Q1,
Q2, Q3 are parallel.
for i = 1, 2, 3, and the
tangent planes to X at Q1,
Q2, Q3 are parallel.  > 0 there exist two
distinct points Q1, Q2 in U
such that |P -Qi| <
> 0 there exist two
distinct points Q1, Q2 in U
such that |P -Qi| <  for i = 1, 2, and the tangent
planes to X at Q1 and Q2
are equal.
for i = 1, 2, and the tangent
planes to X at Q1 and Q2
are equal.  > 0 and
d > 0, there exists a point Q in U and
a D > d such that
|P - Q| <
> 0 and
d > 0, there exists a point Q in U and
a D > d such that
|P - Q| <  and
Q is a swallowtail point of the parallel surface to X at
distance D .
and
Q is a swallowtail point of the parallel surface to X at
distance D .  > 0 there exists Q in U
such that |P - Q| <
> 0 there exists Q in U
such that |P - Q| <
 and Q is an inflection point of an
asymptotic curve of X.
and Q is an inflection point of an
asymptotic curve of X.

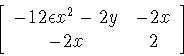
 -1/4,
this vector is tangent to the parabolic curve if and only if
t = 0, where the Gauss map has a cusp. If
-1/4,
this vector is tangent to the parabolic curve if and only if
t = 0, where the Gauss map has a cusp. If
 V : U->R be
the composition of X with the orthogonal projection to the line
spanned by V:
V : U->R be
the composition of X with the orthogonal projection to the line
spanned by V: