0 then X is regular, and for
x > 0 the unif normal is
The parabolic set occurs when
0 = 
= -f'(x) f"(x),
i.e. at extrema or at inflections of the profile curve. Furthermore,
grad = (-(f"(x))2 - f'(x) f'''(x), 0),
so Ñ is good if f"(x) = 0 implies
f'(x) 0 and
f'''(x) 0.
If x0 is a value for which f''(x0) = 0, then the parabolic curve can be parametrized by x(t) = x0, y(t) = t, and we obtain
0 and
f'''(x0) 0, then the Gauss map
has an ordinary fold along the parabolic curve. For example, these
conditions are satisfied by the bell surface:
On the other hand, if x0 is a value for which
f'(x0) = 0 and
f"(x0) 0, then the Gauss map
is good, but not excellent, because the parabolic curve is
parametrized by x(t) = x0,
y(t) = t, and
N(t) = (0, 0) for all t. An example is the top
of a torus of revolution:
Let 
be a regular space curve wit curvature nowhere zero.
Define the canal surface about of radius r to be
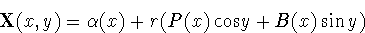
where P and B are the principal normal and the binormal of the
curve . To find the normal of the surface X, we form
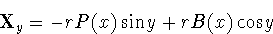
where 
and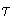 
are the curvatuer and torsion of ,
and s is the arclength along . Then
so the parabolic set occurs when the two vectors
are linearly dependent, i.e. when
cos y = 0. This occurs at the curves
x(t) = t,
y(t) = ±
/2, for which we have
A straightforward calculation gives the Gaussian curvature
K = cos y/(r (rcos y - 1))
and
K/y = sin y/(r (rcos y - 1)2),
so K = 0 implies grad K 0,
since 0. Therfore the Gauss map is good. Now
taking derivatives with respect to t, we obtain
so N' = 0 if and only if 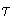= 0 and
then N" = 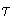's'P. So the Gauss
map N is excellent if 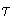' 0 whenever
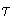= 0, and then N(x, y) has a
cusp at (t ,±/2) if and only if
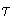(t) = 0.
For example consider the warped torus, a canal surface of the space curve
(t) = (cos t, sin t, 
sin(nt))
where n is an integer, n 
2. The
curvature of is nowhere zero, since
(s')3 = |(' x ")| 1.
Furthermore
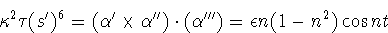
so 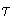= 0 if and only if
t = /2n, 3/2n, ...,
(4n - 1)/2n, provided that
0. Taking derivatives of
2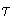(s')^6 and
n(1 - n2)cos nt
shows that tau = 0 implies 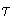' 0, so
long as 0. Therfore a canal surface of has
an excellent Gauss map, with 4n cusps. For = 0 a
canal surface of is a torus of revolution, and each component
of the parabolic curve is collapsed to a point by the Gauss map.
