Previous: Chapter 5: Projections to lines
Up: Table of Contents
Next: Chapter 7: Projections to planes


Chapter 6

Focal and parallel surfaces



For an embedding X: U -> R3 of a domain U of R2 into 3-space, the parallel surface at distance r is the image of the parallel map Xr: U -> R3 defined by Xr(P) = X(P) + rN(P), where N = (Xx x Xy)/|Xx x Xy| is the unit normal of X. The parallel surface can be thought of as a "wave front" at distance r from the image of X. Let S(Xr) be the set of singular points of Xr.

S(Xr) = {P U | rank d(Xr) < 2}

Then P S(Xr) if and only if r is a principal radius of curvature of X at P with focal point Xr(P). So the union of the singular sets of parallel surfaces of X is the focal surface F.

Let be the normal bundle of X:

= {(V, P) R3 x U | V is normal to X at P}

and let : -> R3 be defined by (V, P) = X(P) + V. The focal surface F is the set of critical values of . If the normal lines are thought of as rays of light streaming out from the surface, then the focal surface is the "caustic" of this bundle of rays. In purely geometric terms, the focal surface is the envelope of the family of normal lines of the embedding X [T2].

Gauss thought of his mapping N as assigning to each point of a surface a point on the sphere at infinity, analogous to the celestial sphere used in navigation and surveying [Ba, p. 45]. Let p: R3 - {0} -> S2 be radial projection. For r sufficiently large, the parallel surface to X at distance r does not pass through the origin, so p ° Xr is defined, and the limit as r goes to infinity of (p ° Xr) is N. In other words, the Gauss map is the parallel map at infinity. Another way to see this is to consider the family of maps It: U -> R3, 0 t < 1:

It(P) = (1-t) X(P) + t N(P)

= (1-t)[X(P) + t/(1-t) N(P)]

The family It is the linear interpolation between the embedding X and its Gauss map N. Each map I for 0 t < 1 is homothetic to the parallel map Xr, r = t/(1 - t) (cf. [Ba]). Thus the critical values of the Gauss map are the focal points at infinity.

Now consider an immersion X: Mn -> Rn+1 of the smooth n-manifold M in Euclidean (n + 1)-space. Let 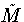be the unit normal bundle of X:

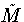= {(V, P) S2 x M|V is normal to X at P}

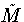As observed in chapter 5, is the oriented double cover of M. For each real number r > 0, the parallel map to X at distance r is

Xr: 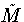 -> Rn+1, Xr(V, P) = X(P) + rV

The image of Xr is the parallel hypersurface of X at radius r. The union of the singular sets of parallel surfaces of X is the focal hypersurface F. If is the normal bundle of X, and : -> Rn+1, (V, P) = X(P) + V, the focal hypersurface F is the set of critical values of .

For each point A Rn+1 let DA: M -> R be the radial distance squared function from A:

DA = |A - X(P)|2

For almost all A Rn+1, the function DA is a nondegenerate Morse function on M [Mi, p. 36]. Following Thom [T4] and Porteous [Por1], consider the family of all such radial functions parametrized by Rn+1:

D : Rn+1n -> Rn+1 x R, D(A, P) = (A, DA(P))

The critical set C of the family D is the set of pairs (A, P) such that the vector A - X(P) is normal to the immersion X at P, so C is identified with the normal bundle , and the catastrophe map :C -> Rn+1 is just the map :  -> Rn+1. Therefore the focal surface of X is the bifurcation set of the family of radial distance functions D.

To relate the map :  -> Rn+1 and the Gauss map N: 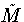-> Sn, we fit the two families D and together, following Looijenga [Lo], [Wa2, p.713]. Consider the family of functions

L: Sn+1 x Mn -> Sn+1 x R

L((a1, ..., an+2), P) = an+2|X(P)|2 - 2 (a1, ..., an+1) . X(P)

= an+2 D(1/(an+2(a1, ..., an+1), P) - 1/(an+2|(a1, ..., an+1)|2

The restriction of L to Sn+1+ x M = {((a1, ..., an+2), P)| an+2  0} [or to Sn+1- x M = {((a1, ..., an+2), P)| an+2 < 0}] is a family equivalent to D. The restriction of L to Sn+10 x M = { ((a1, ..., an+2), P) | an+2 = 0} is equivalent to the family . Let LA(P) = L(A, P).

Theorem 6.1 (Looijenga). Let M2 be a smooth surface. For an open dense subset B of the space of immersions X: M2 -> R3, the germ at (A, P) of the family L is a versal unfolding of the germ of LA at P for all (A, P) S3 x M2.

Proof See [Lo] and [Wa2]. Looijenga proves the equivalent statement that the germ of the mapping L:S3 x M2 -> S3 x R is stable. (the subset B consists of all immersions whose jet extensions are transverse to a certain Whitney stratification of a jet space).

For X B, the singularities of the focal set F are cuspidal edges, swallowtails, elliptic umbilics, and hyperbolic umbilics. The umbilic singularities occur precisely at the foci of the umbilic points of the immersion. A discussion of the geometry of the focal set can be found in Porteous' paper [Por1], which was a starting point for our research on the extrinsic geometry of surfaces. Porteous calls the cuspidal edges of the focal surface ribs. The corresponding curves on the surface M are the ridges of the immersion X (cf. chapter 3). If the map :  -> R3 has a cusp at (V, P) , then P is a ridge point of X, and 1/|V| is the principal curvature associated with the ridge at P.

This description does not include those ridge points with associated principal curvature zero, which correspond to ribs at infinity. To include these points, consider the bifurcation set F Sn+1 of the family L. For the diffeomorphism F: Sn+1+ -> Rn+1, f((a1, ..., an+1)) = 1/an+2 (a1, ..., an+1), we have f(F~ S3+) = F. For X B, the singularities of F~ are cuspidal edges, swallowtails, elliptic umbilics, and hyperbolic umbilics. If the catastrophe map ~ of L has a cusp at (A, P) Sn+1 x Mn, then P is a ridge point of X with associated principal curvature an+2/|(a1, ..., an+1)|. The singularities of F~ Sn+10 correspond to singularities at infinity of F.

For example, the focal surface of the monkey saddle has an elliptic umbilic at infinity. (the monkey saddle is an example of an immersion X: M2 -> R2 such that X is in B but X is not in A. The inclusion of the unit sphere in R3 is an example of an immersion in A but not B.)

The following theorem implies theorem 3.1(d).

Theorem 6.2 If P is a cusp of the Gauss map of X: M2 -> R3, then P is a ridge point of X with associated principal curvature zero. If X A then the cusps of the Gauss map of X are the only points of M with this property.

Proof P is a cusp of the Gauss mapping of X if and only if (V, P) is a cusp of the catastrophe map of the family , where V is a unit normal vector to X at P. The 2-parameter family is equivalent to the restriction of the 3-parameter family L to S30 x M2. therefore if has a cusp at (V, P), then ~ has a cusp at (i(V), P), where i: S2 -> S3 is the inclusion and is the catastrophe map of the family L. So P is a ridge point of X with associated principal curvature zero. Moreover, the ridge curve crosses the parabolic curve transversely at P.

If X A then the germ at (V, P) of is either regular, a fold, or a cusp. If one of the principal curvatures of X at P is zero, then the germ at (V, P) of is a fold or a cusp. If it is a fold, then the germ of ~ at (i(V), P) is a fold, so P is not a ridge point.

Theorem 6.3 If P is a cusp of the Gauss map of X: M2 -> R3, then given  > 0 and d > 0, there exists a point Q U and a D > d such that |P - Q| <  and Q is a swallowtail point of the parallel surface to X at distance D. If X A then the cusps of the Gauss map X are the only points of M with this property.

Proof The parallel map Xr has a cusp at (V, Q) 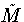if and only if the map : -> R3 has a fold at (rV, Q). So a parallel surface has a cuspidal edge only where it meets the focal surface, and swallowtails only where it meets the cuspidal edge of the focal surface.

If P is a Gaussian cusp, then P is a ridge point with associated principal curvature zero (theorem 6.2). So a point Q near P on the ridge curve through P has the desired property. If X A then the cusps of the Gauss map are the only points with this property, by theorem 6.2.

The following corollary implies theorem 3.1(f).

Corollary 6.4 If P is a cusp of the Gauss map of X: M2 -> R3, then for any point A in R3 which is not on the tangent plane to X at P, the point P is a swallowtail point of the pedal surface of X from A. If X A then the cusps of the Gauss map X are the only points of M with this property.

Proof Consider f: S2 x R -> R3, f(V, t) = A + tV. Since the Gauss map N: 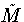 -> S2 is the catastrophe map of the family : S2 x M -> S2 x R, the cusps of N are the swallowtails of |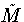. But f((M)) is precisely the pedal surface of X from A.

Notice that this result gives a more visual proof of the bitangent plane characterization of Gaussian cusps, since a swallowtail point of the pedal surface corresponds to a limit of bitangent planes of X.

The point P is a critical point of the distance function DA if and only if the sphere through X(P) centered at A is tangent to the immersion X at P. The point P is a degenerate critical point of DA if and only if this sphere SA has unusual contact with X at P. For example, if A is a focal point of X at P then DA has Milnor number two at P, and SA has stationary contact with X at P. As the point A goes to infinity in the direction V S2, the sphere SA approaches the plane perpendicular to V, and spherical contact becomes the planar contact discussed at the end of chapter 5.

Lagrange and Legendre singularities [A2], [A3], [A4], [AGV], [Wa2]

Lagrangian singularities are generalizations of the singularities which occur in the normal map : N -> Rn+1 of an immersion X: Mn -> Rn+1. The map is an example of a Lagrange mapping, and the set of critical values of (the envelope of the family of normal lines of X, i.e. the focal surface of X) is its caustic [A3].

Recall that the normal map is the catastrophe map of the family D of radial distance-squared functions. In general, if F: Q x M -> Q x R is a family of real-valued functions on M parametrized by Q, then the catastrophe map : C -> Q is Lagrangian (cf. [Wa2, lemma 1, p. 716]). The caustic of is the bifurcation set of the family F. In particular, the Gauss mapping of an immersed hypersurface of Euclidean space is a Lagrange mapping, since it is the catastrophe map of the family of projections to lines (Chpater 5). (Cf. [Wa2, prop. 4, p. 720])

Legendre singularities are generalizations of the singularities which occur in parallel surfaces of an immersed hypersurface of Euclidean space. The parallel map Xr: M -> Rn+1 of the immersion X: M -> Rn+1 is an example of a Legendre mapping, and its image (the parallel hypersurface of X at distance r) is its front [A2].

If F: Q x M -> Q x R is a family of functions with critical set CQ x M, the map F|C is Legendre [A2, thm. 18, p. 33]. For example, for an immersion X: Mn -> Rn+1, consider the family F:Sn x M -> Sn x R of projections to lines. Choose a point A Rn+1 and define f: Sn x R -> Rn+1 by f(V, t) = A +otV. The critical set C of F is M, and f(F(C)) is the pedal surface (from the point A) of the immersion X. Thus the pedal surface of an immersion has Legendre singularities (away from the point A).

A survey of the classification of simple Lagrange and Legendre singularities is given by Arnold in his paper "Critical points of smooth functions" [A3]. An excellent description of the geometry and physics of Lagrange and Legendre singularities is given in Arnold's book Mathematical Methods of Classical Mechanics [A4].

Arnold has communicated to us the following elegant method for dealing with Gauss maps and dual hypersurface singularities using Lagrange and Legendre geometry. The set L of oriented affine lines in Euclidean space Rn is canonically isomorphic with the symplectic manifold T*Sn-1, the dual tangent space of the unit (n-1)-sphere. An isomorphism from L to the tangent space TSn-1 is identified with T*Sn-1 using the Euclidean metric (V -> <V, .>). An easy computation shows that if X: Mn-1 -> Rn is an immersion, then the map N which assigns to P M the normal line to X at P is a Lagrangian immersion of M in L. The Gauss map is the Lagrangian map associated with the Lagrangian immersion N, i.e. the composition of N with projection from L = T*Sn-1 to Sn-1. (Cf. [A4, chapter 8 and appendix 12])

The contractification of the symplectic manifold T*Sn-1 is the contact manifold h consisting of all hyperplanes (contact elements) in the tangent bundle of real projective space RPn. (H can be identified with PT*RPn, the projectivized cotangent bundle of RPn.) The Legendre fibration N -> (RPn)* (the dual projective space) assigns to each tangent hyperplane the (n-1)-dimensional projective space to which it is tangent. If X: Mn-1 -> RPn is an immersion, then the map T which assigns to P M the tangent hyperplane to X at P is a Legendre immersion of M in H. The dual hypersurface X*: M -> (RPn)* is the Legendre map associated with T, i.e. the composition of T with the Legendre fibration N -> (RPn)* (cf. [A4, appendix 4]).

Previous: Chapter 5: Projections to lines
Up: Table of Contents
Next: Chapter 7: Projections to planes