 V: Mn -> gV
be the composition of X with orthogonal projection to
gV:
V: Mn -> gV
be the composition of X with orthogonal projection to
gV:
Let
X: Mn -> Rn+1
be an immersion. For each unit vector V in
Rn+1, let gV be
the hyperplane through the origin perpendicular to V, and let
 V: Mn -> gV
be the composition of X with orthogonal projection to
gV:
V: Mn -> gV
be the composition of X with orthogonal projection to
gV:
 V(P) = X(P) - (X(P) . V) V
V(P) = X(P) - (X(P) . V) V
 *:Sn
x Mn ->
TSn,
*:Sn
x Mn ->
TSn,  *(V, P) = (V,
*(V, P) = (V,  V(P))
V(P))
 * is the set of pairs
(V, P) such that V is parallel to the
tangent hyperplane to X at P, so C is
identified with the unit tangent sphere bundle of X.
* is the set of pairs
(V, P) such that V is parallel to the
tangent hyperplane to X at P, so C is
identified with the unit tangent sphere bundle of X.
Since the tangent bundle of Sn is
trivial over the complement of any point V0  Sn, the
restriction of
Sn, the
restriction of  * to
(Sn - {V0}) x Mn
is an unfolding of
* to
(Sn - {V0}) x Mn
is an unfolding of  V for all
V
V for all
V  V0. Since
V0. Since
 V is a mapping of
n-manifolds, its singularities can be more complicated than
the singularities of a real-valued function (such as the height
function gV studied in chapter 5). Since
V is a mapping of
n-manifolds, its singularities can be more complicated than
the singularities of a real-valued function (such as the height
function gV studied in chapter 5). Since
 V is the composition of the
immersion
X: Mn -> Rn+1
with the orthogonal projection
Rn+1 -> gV,
it follows that
V is the composition of the
immersion
X: Mn -> Rn+1
with the orthogonal projection
Rn+1 -> gV,
it follows that  V has kernel
rank at most one. But
V has kernel
rank at most one. But  V may
have cuspoid (Morin) singularities of arbitrarily high order. To get
a geometric interpretation of these singularities, we first review
their definition.
V may
have cuspoid (Morin) singularities of arbitrarily high order. To get
a geometric interpretation of these singularities, we first review
their definition.
Thom [T1] suggested that for a "generic"  mapping f: N -> P one could stratify
the source N by the kernel rank of f. Each
resulting stratum S would in turn be stratified by the kernel
rank of f|S. This process would be
repeated until no new strata were produced. For a generic map
f: Rn -> Rn
of kernel rank at most one, S1(f) denotes
the set of singular points of f,
S1,1(f) = S12(f)
denotes the set of singular points of
f|S1(f), and in general
S1k(f) is the set of
singular points of
f|S1k-1(f).
Also S1k,0(f) denotes
S1k(f) - S1k-1(f).
Thus S1,0(f) is the fold locus of
f, where the kernel field
mapping f: N -> P one could stratify
the source N by the kernel rank of f. Each
resulting stratum S would in turn be stratified by the kernel
rank of f|S. This process would be
repeated until no new strata were produced. For a generic map
f: Rn -> Rn
of kernel rank at most one, S1(f) denotes
the set of singular points of f,
S1,1(f) = S12(f)
denotes the set of singular points of
f|S1(f), and in general
S1k(f) is the set of
singular points of
f|S1k-1(f).
Also S1k,0(f) denotes
S1k(f) - S1k-1(f).
Thus S1,0(f) is the fold locus of
f, where the kernel field  of
Df is not tangent to S1(f).
The locus S1,1(f) where
of
Df is not tangent to S1(f).
The locus S1,1(f) where  is tangent to S1(f) is
then subdivided into the cusp points
S1,1,0(f) where
is tangent to S1(f) is
then subdivided into the cusp points
S1,1,0(f) where  is
not tangent to S1,1(f), and the points
S1,1,1(f) where
is
not tangent to S1,1(f), and the points
S1,1,1(f) where  is
tangent to S1,1(f), and so on. The stratum
S13,0 is the swallowtail points
of f, and S14,0(f) is
the butterfly points of f. The dimension of
S1k(f) is
n - k.
is
tangent to S1,1(f), and so on. The stratum
S13,0 is the swallowtail points
of f, and S14,0(f) is
the butterfly points of f. The dimension of
S1k(f) is
n - k.
Boardman carried out Thom's suggestion rigorously. He defined submanifolds of the infinite jet space J(N, P) whose pullbacks by the jet extension map of f are the desired strata of n. A "generic" map of f is one whose jet extension is transverse to these Boardman submanifolds. It is possible to write down local defining equations for these submanifolds, and so it is possible to stratify nongeneric maps as well. For mappings f:Rn -> Rn of corank 1, it is easy to give an inductive construction of these equations (cf. [Mori] and [Mat] for details). Start with the equations of S1k(f) and the component functions of one map F. Then the n x n minors of the Jacobian matrix DF are the equations of S1k+1(f). To see the connection with kernel vector fields, consider the equations for S1,1(f). They are
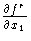 )',
..., (
)',
..., ( )') = 0, 1
)') = 0, 1 r
r  n
n
where (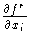 )' denotes
)' denotes 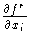 in Df. For a mapping f
of rank n-1, one of the vectors ((
in Df. For a mapping f
of rank n-1, one of the vectors ((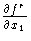 )', ...,(
)', ...,( )') must
span the kernel of Df. Condition (ii) implies that for generic
f (i.e. grad det Df
)') must
span the kernel of Df. Condition (ii) implies that for generic
f (i.e. grad det Df  0 on
S1(f)) this kernel field is tangent to
S1(f).
0 on
S1(f)) this kernel field is tangent to
S1(f).
If f(x1, ...,
xn) = (x1, ...,
xn-1,
fn(x1, ...,
xn)), with grad fn  0, the equations defining
S1k become much simpler. Then
P
0, the equations defining
S1k become much simpler. Then
P  S1k,0(f) if and only if
S1k,0(f) if and only if
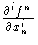 (P) = 0
for 1
(P) = 0
for 1  i
i  k and
k and  (P)
(P)
 0. This allows a direct geometric
interpretation of the Thom-Boardman strata
S1k, 0(
0. This allows a direct geometric
interpretation of the Thom-Boardman strata
S1k, 0( V):
V):
A point P  Mn is in S1k,
0(
Mn is in S1k,
0( V) if and only if the
line through X(P) parallel to V
has kth order contact with the immersion
X at P.
V) if and only if the
line through X(P) parallel to V
has kth order contact with the immersion
X at P.
Since any immersed hypersurface is locally a function graph, this
statement follows from [St, p. 24, (7-4)]. Or we can define the order
of contact of a hypersurface and a line to be m-1, where
m is their intersection multiplicity. This multiplicity
m is the dimension of the real vector space  A/I, where
A/I, where  A is the local ring of germs at
A = X(P) of
A is the local ring of germs at
A = X(P) of  real-valued functions on Rn+1, and
I is the ideal generated by the local defining equations of
X(M) and the line. If this line l is not tangent ot
X(M) at A, then m is one. If it is
tangent, then there are coordinate charts about P in
M and X(P) in Rn+1
so that X(x1, ...,
xn) = (x1, ...,
xn, f(x1, ...,
fn)), and l is spanned by
(0, ..., 0, 1, 0). Then
real-valued functions on Rn+1, and
I is the ideal generated by the local defining equations of
X(M) and the line. If this line l is not tangent ot
X(M) at A, then m is one. If it is
tangent, then there are coordinate charts about P in
M and X(P) in Rn+1
so that X(x1, ...,
xn) = (x1, ...,
xn, f(x1, ...,
fn)), and l is spanned by
(0, ..., 0, 1, 0). Then
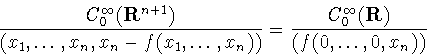
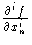 (0) = 0, i
(0) = 0, i k,
k,  (0) = 0. But this is the same
condition given above for P
(0) = 0. But this is the same
condition given above for P  S1k, 0(
S1k, 0( V).
V).
Now we examine the family  * for
X: M2 -> R3
in more detail. The following result implies theorem 3.1(g).
* for
X: M2 -> R3
in more detail. The following result implies theorem 3.1(g).
Theorem 7.1 If P is a cusp of the Gauss map of the
immersion
X: M2 -> R3,
then a line in R3 has order of contact > 2
with X at P. Conversely, if X  A, and P is a parabolic
point of X, and there exists a line in R3
which has order of contact >2 with X at P, then
P is a cusp of the Gauss map of X.
A, and P is a parabolic
point of X, and there exists a line in R3
which has order of contact >2 with X at P, then
P is a cusp of the Gauss map of X.
Proof If P is a parabolic point of X, then after a rigid motion of R3 we may assume that there is a coordinate neighborhood about P on which X has the form
X(x, y) = (x, y,  x2/2 + g(x, y)),
P = (0, 0),
x2/2 + g(x, y)),
P = (0, 0),
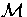 2)3. Here
2)3. Here 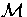 2 is the maximal ideal of the local ring
2 is the maximal ideal of the local ring
 0(R2) of germs at
zero of real-valued functions on R2. The constant
0(R2) of germs at
zero of real-valued functions on R2. The constant
 is the nonzero principal curvature of
X at P, and (x, y,
is the nonzero principal curvature of
X at P, and (x, y,  x2) is the osculating paraboloid of
X at P. The principal direction associated to
x2) is the osculating paraboloid of
X at P. The principal direction associated to  is the x-axis, and the zero principal
curvature direction is the y-axis.
If P is a cusp of the Gauss map N, then P
is the x-axis, and the zero principal
curvature direction is the y-axis.
If P is a cusp of the Gauss map N, then P
 S1, 1(N), so
gyyy(0) = 0, by a computation
using the modified Gauss map Ñ (Chapter 1) and the
equations (i) (ii) above for S1,1(N). But
gyyy(0) = 0 implies that the
y-axis has order of contact
S1, 1(N), so
gyyy(0) = 0, by a computation
using the modified Gauss map Ñ (Chapter 1) and the
equations (i) (ii) above for S1,1(N). But
gyyy(0) = 0 implies that the
y-axis has order of contact  3 with X at 0.
3 with X at 0.
Conversely, if a line has order of contact  2 with X at 0, it must also have order of
contact
2 with X at 0, it must also have order of
contact  2 with the osculating
paraboloid so it must be the y-axis. If the y-axis
has order of contact
2 with the osculating
paraboloid so it must be the y-axis. If the y-axis
has order of contact  3 with
X at 0 then gyyy(0) = 0, so
P
3 with
X at 0 then gyyy(0) = 0, so
P  S1,1(N). Thus if X
S1,1(N). Thus if X  A then P is a cusp of
N.
A then P is a cusp of
N.
In order to relate cusps of Gauss mappings to the geometry of
asymptotic curves, we first investigate the relation between the
singularities of the map  *: S2 x M2 -> TS2
and the second fundamental form of X.
*: S2 x M2 -> TS2
and the second fundamental form of X.
We assume that the immersion X is locally of the form
X(x, y) = (x, y, f(x, y)), grad f(0, 0) = 0
Consider the orthogonal projection to a plane containing the z-axis:
 V(x, y) = (-bx + ay, f(x, y))
V(x, y) = (-bx + ay, f(x, y))
Let Dnf: (R2)n -> R be the symmetric multilinear function whose coefficients are the mixed partial of f of order n.
 S12(
S12( V) iff V is an asymptotic
vector of X at 0.
V) iff V is an asymptotic
vector of X at 0.  S13(
S13( V) iff
D3f(V, V, V) = 0
and 0
V) iff
D3f(V, V, V) = 0
and 0  S12(
S12( V).
V).  S14(
S14( V) iff
D4f(V, V, V, V) = 0
and 0
V) iff
D4f(V, V, V, V) = 0
and 0  S13(
S13( V).
V).
Proof (i) Let
F(x, y) = (-bx + ay, f(x, y),
det D V(x, y)). The
equations which define S12(
V(x, y)). The
equations which define S12( V) are the 2 x 2 minors of
DF. These minors are Df(V),
D2f(V, V), and
D2f(V, (-fy,
fx)). The first and third of these minors
are zero at 0 so only the second is a new condition. But
D2f(V, V) = 0 if
and only if the second fundamental form
II(V, V) = 0, i.e. V is an
asymptotic vector.
V) are the 2 x 2 minors of
DF. These minors are Df(V),
D2f(V, V), and
D2f(V, (-fy,
fx)). The first and third of these minors
are zero at 0 so only the second is a new condition. But
D2f(V, V) = 0 if
and only if the second fundamental form
II(V, V) = 0, i.e. V is an
asymptotic vector.
(ii) The defining equations of S13
are the 2 x 2 minors of DG, where G has
component functions (F, D2f(V,
V)). (It is not necessary to use
D2f(V, (-fy,
fx)) since this function is in the ideal
generated by the components of G.) These minors are in the
ideal generated by the minors of DF, and
D3f(V, V, V). So 0
 S13(
S13( V) if and only if 0
V) if and only if 0  S12(
S12( V) and
D3f(V, V, V).
V) and
D3f(V, V, V).
(iii) has a similar proof.
Now we look at the relation between
S1k( V) and asymptotic curves. Recall that
X(x, y) = (x, y, f(x, y)),
grad f(0, 0) = 0. Assume that (0, 0)
is a hyperbolic point of X, and
V) and asymptotic curves. Recall that
X(x, y) = (x, y, f(x, y)),
grad f(0, 0) = 0. Assume that (0, 0)
is a hyperbolic point of X, and  is an
asymptotic curve of X in the (x, y)
plane, parametrized by arc-length, with
is an
asymptotic curve of X in the (x, y)
plane, parametrized by arc-length, with  '(0) = V. Let
'(0) = V. Let 
 (s) be the
curvature of
(s) be the
curvature of  .
.
 S12, 0(
S12, 0( V) iff
V) iff 
 (0)
(0)  0.
0.  S13,
0(
S13,
0( V) iff
V) iff 
 (0) = 0,
(0) = 0,
 '
' (0)
(0)  0.
0.  S14, 0(
S14, 0( V) iff
V) iff 
 (0) = 0,
(0) = 0,  '
' (0) = 0,
(0) = 0,  ''
'' (0)
(0)  0.
0.
Proof We proceed by the time-honored principle of differentiating something which is identically zero.
(i)  is an asymptotic curve of X if
and only if
is an asymptotic curve of X if
and only if
D2f( (x))[
(x))[ '(s),
'(s),
 '(s)] = 0
'(s)] = 0
so
0 = (D2f( (s))[
(s))[ '(s),
'(s),  '(s)])'
'(s)])'
= D3f( (s))[
(s))[ '(s),
'(s),  '(s),
'(s),  '(s)] + 2 D2f(
'(s)] + 2 D2f( (s))[
(s))[ '(s),
'(s),  ''(s)]
''(s)]
= D3f( (s))[
(s))[ '(s),
'(s),  '(s),
'(s),  '(s)] + 2
'(s)] + 2 
 (s)D2f(
(s)D2f( (s))[
(s))[ '(s),
n(s)]
'(s),
n(s)]
where n is the unit normal vector of  . Now 0
. Now 0  S12,0(
S12,0( V) if and only if
D3f(0)(V, V, V)
V) if and only if
D3f(0)(V, V, V)  0, so 0
0, so 0  S12,0(
S12,0( V) if and only if 2
V) if and only if 2
 (0)
D2f(0)[
(0)
D2f(0)[ '(0), n(0)]
'(0), n(0)] 0, so
0, so 
 (0)
(0) 0. Note that D2f(0)[
0. Note that D2f(0)[ '(0), n(0)]
'(0), n(0)]  0 since
0 since  '(0) and n(0) are orthogonal, for the
only orthogonal conjugate directions at a hyperbolic point are the
principal directions. This proves (i).
'(0) and n(0) are orthogonal, for the
only orthogonal conjugate directions at a hyperbolic point are the
principal directions. This proves (i).
(ii) D3f( (0))[
(0))[ '(0),
'(0),  '(0),
'(0),  '(0)] = 0 iff
'(0)] = 0 iff 
 (0) = 0 iff 0
(0) = 0 iff 0
 S13(
S13( V). Now
V). Now
0 = (D2f( (s))[
(s))[ '(s),
'(s),  '(s)])''
'(s)])''
= D4f( )[
)[ ',
',  ',
',  ',
',
 '] + 3
'] + 3 D3f(
D3f( )[
)[ ',
',  ',
n] + 2
',
n] + 2 D3f(
D3f( )[
)[ ',
',  ',
n]
',
n]
+ 2 2D2f(
2D2f( )[n, n] +
2D2f(
)[n, n] +
2D2f( )[
)[ ',
',  n' +
n' +  'n]
'n]
If s = 0 and 0  S13(
S13( V), then
V), then
0 = D4f(0)[V, V, V, V] +
2D2f(0)[V,  '(0), n(0)]
'(0), n(0)]
 S13,0(
S13,0( V) iff
V) iff  '(0)
'(0)  0.
0.
(iii) Compute 0 = (D2f( (s))[
(s))[ '(s),
'(s),  '(s)])'''.
'(s)])'''.
Now consider the space curve X °  with curvature
with curvature  X °
X °  . Since an asymptotic curve on a surface has
normal curvature zero, its curvature as a space curve equals its
intrinsic curvature. By our choice of coordinates for the immersion
X,
. Since an asymptotic curve on a surface has
normal curvature zero, its curvature as a space curve equals its
intrinsic curvature. By our choice of coordinates for the immersion
X,

 X °
X °  (0) =
(0) =


 (0) provided that
(0) provided that
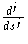

 (0) for
j<i. Thus we have:
(0) for
j<i. Thus we have:
 S12, 0(
S12, 0( V) iff
V) iff  X °
X °  (0)
(0)  0.
0.
 S13, 0(
S13, 0( V) iff
V) iff  X °
X °  (0) = 0,
(0) = 0,  'X °
'X °  (0)
(0)  0.
0.
 S14, 0(
S14, 0( V) iff
V) iff  X °
X °  (0) = 0,
(0) = 0,  'X °
'X °  (0) = 0,
(0) = 0,  ''X °
''X °  (0)
(0)  0.
0.
In geometric terms, if l is the line through P parallel to V, we have:
 S12,0(
S12,0( V) iff V is an asymptotic
vector of X at P, and the corresponding asymptotic
curve X °
V) iff V is an asymptotic
vector of X at P, and the corresponding asymptotic
curve X °  has nonzero
intrinsic curvature at P.
has nonzero
intrinsic curvature at P.
 S13,0(
S13,0( V) iff V is an asymptotic
vector of X at P, and the corresponding asymptotic
curve X °
V) iff V is an asymptotic
vector of X at P, and the corresponding asymptotic
curve X °  has a simple
inflection at P. (Such a line l is called
"flecnodal" in [Sa, 588].
has a simple
inflection at P. (Such a line l is called
"flecnodal" in [Sa, 588].
 S14,0(
S14,0( V) iff V is an asymptotic
vector of X at P, and the corresponding asymptotic
curve X °
V) iff V is an asymptotic
vector of X at P, and the corresponding asymptotic
curve X °  has a simple
"undulation" at P.
has a simple
"undulation" at P.
We can now prove half of theorem 3.1(h).
Theorem 7.5 Let
X: M2 -> R3
be an immersion, with X  A. If P is a parabolic point of X which is
in the closure of the set of asymptotic inflection points of
X, then P is a cusp of the Gauss mapping of
X.
A. If P is a parabolic point of X which is
in the closure of the set of asymptotic inflection points of
X, then P is a cusp of the Gauss mapping of
X.
Proof By corollary 7.4, P is in the closure of
S13,0( V), which is
S13(
V), which is
S13( V). Therefore the line through
X(P) parallel to V has order of contact > 3
with X at P. By theorem 7.1, P is a cusp
of the Gauss mapping.
V). Therefore the line through
X(P) parallel to V has order of contact > 3
with X at P. By theorem 7.1, P is a cusp
of the Gauss mapping.
A more precise analysis of the singularities of the family  * is based on the following result.
* is based on the following result.
Theorem 7.6 (Arnold, Lyashko, Goryunov, Gaffney-Ruas) Let
M2 be a smooth surface. For an open dense subset
C of the space of immersions
X: M2 -> R3,
the germ of the family  * at
(V, P) is a versal unfolding of the germ of
* at
(V, P) is a versal unfolding of the germ of  V at P for all
(V, P)
V at P for all
(V, P)  S2 x M2.
S2 x M2.
For proofs, see [GafR] [A6]. (This result is closely related to
theorem (A) of [Wa2, p. 712]). If the germ of  * at (V, P) is a versal
unfolding of the germ of
* at (V, P) is a versal
unfolding of the germ of  V at
P, then the germ of the mapping
V at
P, then the germ of the mapping  * at (V, P) is stable.
The converse is not true. If the germ of
* at (V, P) is stable.
The converse is not true. If the germ of  * is versal at each point, then the germ of
the Gauss map of X is stable at each point, so C is
a subset of A. Menn's surface
X(x, y) = (x, y, x2 y - x2)
has a stable Gauss map at (0, 0), but
* is versal at each point, then the germ of
the Gauss map of X is stable at each point, so C is
a subset of A. Menn's surface
X(x, y) = (x, y, x2 y - x2)
has a stable Gauss map at (0, 0), but  * is not versal at (0, 0).
* is not versal at (0, 0).
Gaffney and Ruas' proof is based on an explicit classification of
all rank one finitely determined germs of codimension four or less.
For X  C, there are ten
equivalence classes of germs which may occur as germs of
C, there are ten
equivalence classes of germs which may occur as germs of  V at P (see [GafR] [A6]). For
example, if X
V at P (see [GafR] [A6]). For
example, if X  C then
S15(
C then
S15( V) = Ø and
S14(
V) = Ø and
S14( V) is a set of isolated points.
Furthermore, P
V) is a set of isolated points.
Furthermore, P  S14(
S14( V) only if P is hyperbolic.
Therefore a line l in R3 can have order
of contact at most 3 with X at a parabolic point, so theorem
7.1 can be strengthened for X
V) only if P is hyperbolic.
Therefore a line l in R3 can have order
of contact at most 3 with X at a parabolic point, so theorem
7.1 can be strengthened for X  C:
C:
Corollary 7.7 If X  C, then P is a Gaussian cusp if and only if
P is a parabolic point of X and there is a line in
R3 which has third order contact with X
at P.
C, then P is a Gaussian cusp if and only if
P is a parabolic point of X and there is a line in
R3 which has third order contact with X
at P.
Corollary 7.8 If X  C, then P is a Gaussian cusp if and only if
P is a parabolic point of X in the closure of the
set of inflection points of asymptotic curves.
C, then P is a Gaussian cusp if and only if
P is a parabolic point of X in the closure of the
set of inflection points of asymptotic curves.
Proof By the proof of theorem 7.1, if X  C, then P is a cusp of the
Gauss mapping if and only if (V, P)
C, then P is a cusp of the
Gauss mapping if and only if (V, P)  S13(
S13( *), where V is asymptotic at
P. Since
*), where V is asymptotic at
P. Since  * is versal at
(V, P) and (V, P) and
S13 is a codimension 3 singularity,
(V, P)
* is versal at
(V, P) and (V, P) and
S13 is a codimension 3 singularity,
(V, P)  S13(
S13( *) if
and only if there exists a curve
(V(t), P(t)) in
S2 x M2, 0
*) if
and only if there exists a curve
(V(t), P(t)) in
S2 x M2, 0  t
t 
 , such that P(t)
, such that P(t)  S13,0(
S13,0( V(t)) for
t > 0, and
(V(0), P(0)) = (V, P).
The projection of this curve to M2 is a curve of
asymptotic inflection points with P in its closure.
V(t)) for
t > 0, and
(V(0), P(0)) = (V, P).
The projection of this curve to M2 is a curve of
asymptotic inflection points with P in its closure.
Using theorem 7.6 we can also complete the proofs of theorem 3.1(h)
and theorem 3.3. It will be necessary to use a few facts about the
"cusp catastrophe map"  1,1: S1,1(
1,1: S1,1( *) -> S2, the
restriction of the projection
S2 x M2 -> S2.
*) -> S2, the
restriction of the projection
S2 x M2 -> S2.
 C then
C then
 *)
is diffeomorphic to a two-sheeted cover of the double of the manifold
of negative curvature of M.
*)
is diffeomorphic to a two-sheeted cover of the double of the manifold
of negative curvature of M.
 1,1 is the union of
S13(
1,1 is the union of
S13( *) and
the set {(V, P)|P is parabolic and
V is an asymptotic vector at P }.
*) and
the set {(V, P)|P is parabolic and
V is an asymptotic vector at P }.
 1,1 at (V, P) is
equivalent to (x, y3 - x2y). (Note that
this germ is not stable.)
1,1 at (V, P) is
equivalent to (x, y3 - x2y). (Note that
this germ is not stable.)
Proof See [GafR].
Theorem 7.10 If X: M2 -> R3 is an immersion, and P is a cusp of the Gauss mapping, then P is in the closure of the set of asymptotic inflection points of X.
Proof By hypothesis there exists a neighborhood U
of P such that N|U is stable.
Assume that P is the only cusp of
N|U, and the double of the part of
U with negative curvature is a disc. By theorem 7.6 there
exists a sequence of immersions Xn such
that Xn|U converges to
X|U in the Whitney  topology and the family
topology and the family  n* associated to
Xn is versal on U. Since
N is stable on U, we can assume that, for n
sufficiently large the Gauss map Nn of
Xn differs from N by a coordinate
change in the source and target. Thus for n sufficiently
large, the double of the part of U on which
Xn has negative curvature is a disc, so
S1,1(
n* associated to
Xn is versal on U. Since
N is stable on U, we can assume that, for n
sufficiently large the Gauss map Nn of
Xn differs from N by a coordinate
change in the source and target. Thus for n sufficiently
large, the double of the part of U on which
Xn has negative curvature is a disc, so
S1,1( n*) is two discs. Let
Dn be one of these discs. Let
n*) is two discs. Let
Dn be one of these discs. Let  n be the curve on
Dn which consists of points of
S1,1,1(
n be the curve on
Dn which consists of points of
S1,1,1( n*). Let
n*). Let  n be the curve in
Dn lying over the parabolic curve
Sn. The curve
n be the curve in
Dn lying over the parabolic curve
Sn. The curve  n divides Dn
into two discs, each of which projects diffeomorphically to the
negatively curved part of U. By proposition 7.9,
n divides Dn
into two discs, each of which projects diffeomorphically to the
negatively curved part of U. By proposition 7.9,  n crosses
n crosses  n transversely at a single point, which
lies over the cusp of Nn.
n transversely at a single point, which
lies over the cusp of Nn.
The projection of  n to
U is a curve
n to
U is a curve  n which
is smooth except perhaps at the cusp of Nn,
and which consists of inflection points of asymptotic curves of
Xn. Since
n which
is smooth except perhaps at the cusp of Nn,
and which consists of inflection points of asymptotic curves of
Xn. Since  n crosses
n crosses  n transversely at a single point lying
over the cusp of Nn, the limit of
n transversely at a single point lying
over the cusp of Nn, the limit of  n as n goes to infinity
must be an infinite set I containing the cusp of N
in its closure.
n as n goes to infinity
must be an infinite set I containing the cusp of N
in its closure.
Since the jets of  * at the points of
I are in the closure of the jets of
S13(
* at the points of
I are in the closure of the jets of
S13( n*), they must be in
S13(
n*), they must be in
S13( *),
and since N|U is stable, the only parabolic
point of I is the Gaussian cusp P, by theorem 6.5.
By corollary 7.4, all the other points of I are asymptotic
inflections.
*),
and since N|U is stable, the only parabolic
point of I is the Gaussian cusp P, by theorem 6.5.
By corollary 7.4, all the other points of I are asymptotic
inflections.
This proof illustrates a useful technique: first prove a theorem under a stringent genericity condition; then relax this condition, and use the relaxed condition to control the degeneration of the geometry.
Our final characterization of the Gaussian cusps, theorem 3.3,
reflects the relationship between the two "catastrophe maps" of the
family  *. Let
*. Let  1: S1(
1: S1( *) -> S2 be the
"fold catastrophe map" of the family
*) -> S2 be the
"fold catastrophe map" of the family  *,
i.e. the restriction of the projection
S2 x M2 -> S2.
Thus we have a diagram
*,
i.e. the restriction of the projection
S2 x M2 -> S2.
Thus we have a diagram

Proposition 7.11 (Gaffney and Ruas) If X  C then the germ at
(V, P) of
C then the germ at
(V, P) of  1 is
stable for all (V, P)
1 is
stable for all (V, P)  S1(
S1( *).
This germ is singular if and only if P is parabolic.
*).
This germ is singular if and only if P is parabolic.
Proof see [GafR].
So if X  C the
bifurcation set
C the
bifurcation set  of
of  1 is the asymptotic image of the parabolic
curve. By proposition 7.9, the bifurcation set of
1 is the asymptotic image of the parabolic
curve. By proposition 7.9, the bifurcation set of  1,1 is the union of
1,1 is the union of  and the asymptotic image
and the asymptotic image  of the
asymptotic inflection curve. By 7.9(iii) the intersection points of
of the
asymptotic inflection curve. By 7.9(iii) the intersection points of
 and
and  are
precisely the asymptotic images of the Gaussian cusps. In particular,
if X
are
precisely the asymptotic images of the Gaussian cusps. In particular,
if X  C then the
asymptotic image of the parabolic curve of X is regular at
Gaussian cusps. This completes the proof of theorem 3.3.
C then the
asymptotic image of the parabolic curve of X is regular at
Gaussian cusps. This completes the proof of theorem 3.3.
Finally, we finish the proof of theorem 3.2. Let
Immk(2, 3) be the space of k-jets of
immersion of R2 in R3. Since
Immk(2, 3) is a Euclidean space, with
coordinates the partial derivatives of order  k, we can consider algebraic subsets of
Immk(2, 3), i.e. subsets defined by polynomial
equations. Recall that the parabolic image curve of the
immersion
X: R2 -> R3
is the restriction of X to the parabolic curve of X.
k, we can consider algebraic subsets of
Immk(2, 3), i.e. subsets defined by polynomial
equations. Recall that the parabolic image curve of the
immersion
X: R2 -> R3
is the restriction of X to the parabolic curve of X.
Lemma 7.12 If k  4,
there exists an irreducible algebraic subset V of codimension
2 in Immk(2, 3), and a proper algebraic
subset W of V, such that
jkX(0)
4,
there exists an irreducible algebraic subset V of codimension
2 in Immk(2, 3), and a proper algebraic
subset W of V, such that
jkX(0)  V - W if and only if the Gauss mapping
N of X is stable in some neighborhood of 0,
N has a cusp at 0, and the curvature of the parabolic image
curve of X at 0 is nonzero.
V - W if and only if the Gauss mapping
N of X is stable in some neighborhood of 0,
N has a cusp at 0, and the curvature of the parabolic image
curve of X at 0 is nonzero.
Proof It suffices to consider immersion of the form
X(x, y) = (x, y, f(x, y)),
f  (
(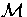 2)2. The set V will be
all k-jets of immersions X with
f(x, y) =1/2
2)2. The set V will be
all k-jets of immersions X with
f(x, y) =1/2 x2 +
a04y4 +
a12xy2 +
a21x2y +
g(x, y) where g
x2 +
a04y4 +
a12xy2 +
a21x2y +
g(x, y) where g  (
(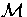 2)3 and
gyyyy(0) = gyyy(0)
= gxyy(0) = gxxy(0) = 0
(cf. the proof of theorem 7.1). The condition that the Gauss map
N be stable is a122 -
2a04
2)3 and
gyyyy(0) = gyyy(0)
= gxyy(0) = gxxy(0) = 0
(cf. the proof of theorem 7.1). The condition that the Gauss map
N be stable is a122 -
2a04
 0, a12
0, a12  0,
0, 
 0. (This
can be verified by direction computation.) To obtain that the
curvature of the parabolic image curve of X at 0 is nonzero,
we have to throw away another proper algebraic subset of V.
0. (This
can be verified by direction computation.) To obtain that the
curvature of the parabolic image curve of X at 0 is nonzero,
we have to throw away another proper algebraic subset of V.
By considering the determinant of the Hessian of f, it is possible to solve implicitly for the 2-jet of the preimage of the parabolic curve in the parametrization plane. It is

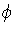 ), where
), where 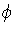 is a
parametrization of the parabolic curve. This 2-jet is determined by
the 2-jets of X and
is a
parametrization of the parabolic curve. This 2-jet is determined by
the 2-jets of X and 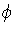 .
Applying the chain rule and standard formulas for the curvature of a
space curve we obtain that the curvature of the parabolic image curve
at 0, for an immersion X such that N has a cusp at
0, is
.
Applying the chain rule and standard formulas for the curvature of a
space curve we obtain that the curvature of the parabolic image curve
at 0, for an immersion X such that N has a cusp at
0, is
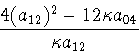
 V, then the curvature of the parabolic image
curve of X at 0 is nonzero if and only if
(a12)2 - 3
V, then the curvature of the parabolic image
curve of X at 0 is nonzero if and only if
(a12)2 - 3 a04
a04  0
0
By [BlW] and lemma 7.12, there exists an algebraic set Y of
codimension 3 in Imm4(2, 3) such that
j4X(P)  Y if and only if (i) N is stable in a
neighborhood of P, and (ii) N has a cusp at
P implies the curvature of the parabolic image curve of
X at P is nonzero. So the Thom transversality
theorem implies the last statement in theorem 3.2, completing the
proof of this theorem.
Y if and only if (i) N is stable in a
neighborhood of P, and (ii) N has a cusp at
P implies the curvature of the parabolic image curve of
X at P is nonzero. So the Thom transversality
theorem implies the last statement in theorem 3.2, completing the
proof of this theorem.
A global version of theorem 3.2, for an immersion
X: M2 -> R3,
is easily obtained by considering the space of 4-jets of immersion
Imm4(M2, R3) as a
fiber bundle over M, with fiber the space of 4-jets at zero
of immersions of R2 in R3.