Previous: Chapter 3: Characterizations of Gaussian cusps
Up: Table of Contents
Next: Chapter 5: Projections to lines
Chapter 4
Singularities of families of mappings
In this section we discuss some of the theory of singularities of maps
used in the rest of the paper.
For smooth manifolds N and P,  (N, P) is
the space of infinitely differentiable mappings from N to P,
with the Whitney
(N, P) is
the space of infinitely differentiable mappings from N to P,
with the Whitney  topology [GolG, p. 42]. Two maps
f, g
topology [GolG, p. 42]. Two maps
f, g 
 (N, P)
are isomorphic if there exist diffeomorphisms
(N, P)
are isomorphic if there exist diffeomorphisms 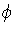 of N and
of N and  of P such that g =
of P such that g =  ° f °
° f ° 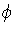 -1. A map f
-1. A map f 
 (N, P) is stable if f has a
neighborhood U in
(N, P) is stable if f has a
neighborhood U in  (N, P) such that every map
g
(N, P) such that every map
g U is isomorphic to f. In other
words, the orbit of f under the action of the group
U is isomorphic to f. In other
words, the orbit of f under the action of the group  = Diff N x Diff P is open in
the Whitney topology [GolG, p. 72].
= Diff N x Diff P is open in
the Whitney topology [GolG, p. 72].
A q-parameter unfolding of the mapping
f0 
 (N, P) is a
(N, P) is a  mapping
F: Rq x N -> Rq x P
of the form
F(u, x) = (u, f(u, x)),
with
f(0, x) = f0(x).
If h
mapping
F: Rq x N -> Rq x P
of the form
F(u, x) = (u, f(u, x)),
with
f(0, x) = f0(x).
If h 
 (Rr, Rq) with
h(0) = 0, the pull-back
h*F is the r-parameter unfolding of
f0 given by (h*F)(v, x) = (v, f(h(v),
x)). Two q-parameter unfoldings F1 and
F2 of the same function f0 are
isomorphic if F2 =
(Rr, Rq) with
h(0) = 0, the pull-back
h*F is the r-parameter unfolding of
f0 given by (h*F)(v, x) = (v, f(h(v),
x)). Two q-parameter unfoldings F1 and
F2 of the same function f0 are
isomorphic if F2 =  ° F1 °
° F1 ° 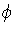 -1, where
-1, where 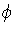 (resp.
(resp.  ) is a
q-parameter unfolding of the identity of N
(resp. P). More generally, F1 and
F2 are equivalent if there is a
diffeomorphism h of Rq such that
F2 is isomorphic to
h*F1. An unfolding F of
f0 is versal if every other unfolding of
f0 is isomorphic to a pull-back of F. (These
definitions are taken from [Mar, p. 6].) A
theorem of Thom and Mather asserts that a q-parameter unfolding
of f0 is versal if and only if the associated map
R^q ->
) is a
q-parameter unfolding of the identity of N
(resp. P). More generally, F1 and
F2 are equivalent if there is a
diffeomorphism h of Rq such that
F2 is isomorphic to
h*F1. An unfolding F of
f0 is versal if every other unfolding of
f0 is isomorphic to a pull-back of F. (These
definitions are taken from [Mar, p. 6].) A
theorem of Thom and Mather asserts that a q-parameter unfolding
of f0 is versal if and only if the associated map
R^q ->  (N, P) is
transverse to the
(N, P) is
transverse to the  -orbit of f0 at
f0 (cf. [Mar, th. 3.3]).
A family of
-orbit of f0 at
f0 (cf. [Mar, th. 3.3]).
A family of  mappings from N to P
parametrized by a smooth manifold q is a
mappings from N to P
parametrized by a smooth manifold q is a  map
F: Q x N -> Q x P of the form
F(u, x) = (u, f(u, x)). If
fu(x) = f(u, x), the introduction of a coordinate
chart about u in Q determines an unfolding of fu
defined by F. Different charts about u determine equivalent
unfoldings of fu In other words, a family of
map
F: Q x N -> Q x P of the form
F(u, x) = (u, f(u, x)). If
fu(x) = f(u, x), the introduction of a coordinate
chart about u in Q determines an unfolding of fu
defined by F. Different charts about u determine equivalent
unfoldings of fu In other words, a family of  mappings defines an unfolding of each of its members.
mappings defines an unfolding of each of its members.
The pull-back of a family F by a map h: Q' -> Q
is defined by
(h*F)(v, x) = (v, f(h(v), x)). Two
families F1 and F2 parametrized by Q
are equivalent if there is a diffeomorphism h of Q, a
family of diffeomorphisms 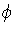 of N
parametrized by Q, and a family of diffeomorphisms
of N
parametrized by Q, and a family of diffeomorphisms  of P parametrized by Q, such that
F2 =
of P parametrized by Q, such that
F2 = 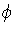 ° (h*F1) °
° (h*F1) ° 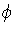 -1. A family is versal if it defines a
versal unfolding of each of its members.
-1. A family is versal if it defines a
versal unfolding of each of its members.
For x  N and y
N and y  P, consider the space of all
P, consider the space of all  maps f:N -> P such that f(x) = y. The
space of germs
maps f:N -> P such that f(x) = y. The
space of germs  (N, P)(x, y)
is the quotient of this space by the equivalence relation:
f ~ g if there is a neighborhood U of x in
N such that f|U = g|U. The
equivalence class of f is called the germ of f at x.
Introducing coordinate charts about x and y,
(N, P)(x, y)
is the quotient of this space by the equivalence relation:
f ~ g if there is a neighborhood U of x in
N such that f|U = g|U. The
equivalence class of f is called the germ of f at x.
Introducing coordinate charts about x and y,  (N, P)(x, y) is identified with
(N, P)(x, y) is identified with  (Rn, Rp)(0,
0) =
(Rn, Rp)(0,
0) =  (n, p)0. Stable germs
and versal unfoldings of germs are defined in a similar manner as for
functions (see [Mar, p. 6]).
(n, p)0. Stable germs
and versal unfoldings of germs are defined in a similar manner as for
functions (see [Mar, p. 6]).
A central problem of singularity theory is the classification of
germs up to isomorphism. Important examples of stable germs are the
cuspoids (or Morin singularities) in  (n, k+1), n > k> 0, with normal form
(n, k+1), n > k> 0, with normal form


where r < k + 1 and  j = ±1 (cf. [Mori]). If r = 1 the
germ is a fold, r = 2 is a cusp, r = 3 is a
swallowtail, and r = 4 is a butterfly. Much work
has been done on classifying the stable map germs (e.g. by Mather and
Damon).
j = ±1 (cf. [Mori]). If r = 1 the
germ is a fold, r = 2 is a cusp, r = 3 is a
swallowtail, and r = 4 is a butterfly. Much work
has been done on classifying the stable map germs (e.g. by Mather and
Damon).
A germ f 
 (n, p)0 is finitely determined if
there is an integer k such that any germ with the same k-jet
(i.e. the same partial derivatives through order k) is isomorphic
to f. A germ is finitely determined if and only if it has a versal
unfolding. The minimum number c of parameters in a versal
unfolding of f is the codimension of f, and a
c-parameter versal unfolding of f is called a universal
unfolding of f (cf. [Mar]). The codimension of f equals the
codimension of the
(n, p)0 is finitely determined if
there is an integer k such that any germ with the same k-jet
(i.e. the same partial derivatives through order k) is isomorphic
to f. A germ is finitely determined if and only if it has a versal
unfolding. The minimum number c of parameters in a versal
unfolding of f is the codimension of f, and a
c-parameter versal unfolding of f is called a universal
unfolding of f (cf. [Mar]). The codimension of f equals the
codimension of the  -orbit of f in
-orbit of f in  (n, p)0. Techniques for classifying
finitely determined germs have been recently work out (e.g. by
Gaffney, DuPleissis, and Martinet).
(n, p)0. Techniques for classifying
finitely determined germs have been recently work out (e.g. by
Gaffney, DuPleissis, and Martinet).
The classification of finitely determined germs leads to a
classification of the singularities of versal families of mappings.
Thom and Mather's transversality criterion for versal unfoldings
implies that only finitely determined germs of codimension of most
q can appear as members of a versal q-parameter unfolding. The
classification of finitely determined germs of codimension  q allows one to write down normal forms
for the members of any q-parameter unfolding , and in fact one can
get a normal form for the unfolding itself.
q allows one to write down normal forms
for the members of any q-parameter unfolding , and in fact one can
get a normal form for the unfolding itself.
Thom-Zeeman catastrophe theory is the study of singularities
of families of real-valued functions
F: Q x N -> Q x R. (an introduction to
the geometry of catastrophes is given in Callahan's survey article
``Sketching catastrophes'' [C2].) The critical set (or
catastrophe manifold) of the family F is the set
C = {(u, x)  Q x N|
Q x N|  F/
F/ x (u, x) = 0}. If F
is versal, then C is a smooth manifold of the same dimension q
as Q. The catastrophe map of the family F is the
projections
x (u, x) = 0}. If F
is versal, then C is a smooth manifold of the same dimension q
as Q. The catastrophe map of the family F is the
projections  : C -> Q. The bifurcation
set of F is the image in Q of the singular set of
: C -> Q. The bifurcation
set of F is the image in Q of the singular set of  (the set of points of C at which
(the set of points of C at which  has rank less than q). As the parameter u
crosses the bifurcation set F, the number of critical points of the
function fu changes
(F(u, x) = (u, fu(x))).
has rank less than q). As the parameter u
crosses the bifurcation set F, the number of critical points of the
function fu changes
(F(u, x) = (u, fu(x))).
A family of real-valued functions
F: Q x N -> Q x R is versal if and
only if F is a stable mapping (cf. [Mar]). However, the catastrophe
map of a versal family is not necessarily stable. Let 

 (q, q)0 be the germ at zero of a
catastrophe map of a versal q-parameter unfolding of a germ f
(q, q)0 be the germ at zero of a
catastrophe map of a versal q-parameter unfolding of a germ f

 (n, 1). If
q = 1,
(n, 1). If
q = 1,  is either regular (i.e. rank q)
or a Morse singularity. If q = 2,
is either regular (i.e. rank q)
or a Morse singularity. If q = 2,  is
either regular, a fold, or a cusp. If q = 3,
is
either regular, a fold, or a cusp. If q = 3,  is regular, a fold, a cusp, a swallowtail, or an
umbilic. Umbilic germs in
is regular, a fold, a cusp, a swallowtail, or an
umbilic. Umbilic germs in  (3, 3)0 are
not stable. Descriptions of these catastrophes can be found in
several sources: [T4, Chapt. 5], [C1], [C2], [PosS, Chapt. 9], [Wo].
The name of the germ
(3, 3)0 are
not stable. Descriptions of these catastrophes can be found in
several sources: [T4, Chapt. 5], [C1], [C2], [PosS, Chapt. 9], [Wo].
The name of the germ  is also used to refer to
the germ f being unfolded (e.g. f(x) = x4 is
called a cusp, because the catastrophe map of the universal unfolding
has a cusp singularity.) In chapter 5 we shall see why Thom chose the
name "umbilic" for the simplest unstable catastrophe map germs.
is also used to refer to
the germ f being unfolded (e.g. f(x) = x4 is
called a cusp, because the catastrophe map of the universal unfolding
has a cusp singularity.) In chapter 5 we shall see why Thom chose the
name "umbilic" for the simplest unstable catastrophe map germs.
Since finitely determined germs can be classified, there is no
reason to consider only families of real-valued functions from the
viewpoint of catastrophe theory. Given a family
F: Q x N -> Q x P
and a closed subset S of  (n, P)0 such that
(n, P)0 such that  S = S, one can consider the
set C = {(u, x)
S = S, one can consider the
set C = {(u, x)  Q x N| the germ of
fu at x is in S}, and the associated
projection map
Q x N| the germ of
fu at x is in S}, and the associated
projection map  : C -> Q. In other words,
there is a ``catastrophe map'' for
: C -> Q. In other words,
there is a ``catastrophe map'' for  (n, p)0. Finally, since
the theory is local, it applies equally well to a ``twisted'' family
parametrized by Q, i.e. a
(n, p)0. Finally, since
the theory is local, it applies equally well to a ``twisted'' family
parametrized by Q, i.e. a  mapping
F:A -> B where
a:A-> Q and
B:B -> Q are smooth fiber bundles over
Q , and
B ° F = a. These
generalizations of catastrophe theory have been developed by Gaffney
and Ruas [GafR], Kergosien [Ke3], and Arnold et al. [AGV]. These generalizations will be used in
chapter 7.
mapping
F:A -> B where
a:A-> Q and
B:B -> Q are smooth fiber bundles over
Q , and
B ° F = a. These
generalizations of catastrophe theory have been developed by Gaffney
and Ruas [GafR], Kergosien [Ke3], and Arnold et al. [AGV]. These generalizations will be used in
chapter 7.
Previous: Chapter 3: Characterizations of Gaussian cusps
Up: Table of Contents
Next: Chapter 5: Projections to lines
 (N, P) is
the space of infinitely differentiable mappings from N to P,
with the Whitney
(N, P) is
the space of infinitely differentiable mappings from N to P,
with the Whitney  topology [GolG, p. 42]. Two maps
f, g
topology [GolG, p. 42]. Two maps
f, g 
 (N, P)
are isomorphic if there exist diffeomorphisms
(N, P)
are isomorphic if there exist diffeomorphisms 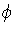 of N and
of N and  of P such that g =
of P such that g =  ° f °
° f ° 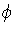 -1. A map f
-1. A map f 
 (N, P) is stable if f has a
neighborhood U in
(N, P) is stable if f has a
neighborhood U in  (N, P) such that every map
g
(N, P) such that every map
g U is isomorphic to f. In other
words, the orbit of f under the action of the group
U is isomorphic to f. In other
words, the orbit of f under the action of the group  = Diff N x Diff P is open in
the Whitney topology [GolG, p. 72].
= Diff N x Diff P is open in
the Whitney topology [GolG, p. 72].


 j = ±1 (cf. [Mori]). If r = 1 the
germ is a fold, r = 2 is a cusp, r = 3 is a
swallowtail, and r = 4 is a butterfly. Much work
has been done on classifying the stable map germs (e.g. by Mather and
Damon).
j = ±1 (cf. [Mori]). If r = 1 the
germ is a fold, r = 2 is a cusp, r = 3 is a
swallowtail, and r = 4 is a butterfly. Much work
has been done on classifying the stable map germs (e.g. by Mather and
Damon).
 q allows one to write down normal forms
for the members of any q-parameter unfolding , and in fact one can
get a normal form for the unfolding itself.
q allows one to write down normal forms
for the members of any q-parameter unfolding , and in fact one can
get a normal form for the unfolding itself.
 F/
F/ : C -> Q. The bifurcation
set of F is the image in Q of the singular set of
: C -> Q. The bifurcation
set of F is the image in Q of the singular set of