English version

Il movimento genera la forma, la forma genera il movimento. Ogni punto, ogni linea, ogni superficie, ogni corpo, ogni ombra, ogni luce e ogni colore sono forme generate dal movimento, che generano a loro volta movimento. [Itten 1921]

INTRODUZIONE
Il movimento artistico Bauhaus, che prende il nome dalla scuola fondata dall'architetto Walter Gropius nel 1919, occupa certamente un posto di rilievo tra le correnti che nel ventesimo secolo hanno avuto come obiettivo il connubio tra arte e razionalità. Gli artisti che l'hanno fondato e ne hanno fatto successivamente parte non hanno mai trascurato di affiancare materie tecniche ai loro studi artistici. La geometria e la matematica in genere hanno avuto ampio spazio nelle loro scuole, e di conseguenza, ad ogni livello artistico (pittura, scultura , manufatti tessili,…), vasta è la produzione di opere in cui risulta evidente una chiave di lettura di tipo matematico-geometrico [De Michelis e Kohlmeyer 1996; Droste 1994; BAB 1999].

A questo proposito risulta intrigante il progetto per la Torre del Fuoco di Johannes Itten, uno dei più importanti esponenti del Bauhaus (Figura 1). Il progetto, ampiamente citato in uno dei suoi Tagebücher (Diari) [Badura-Triska 1990], è stato realizzato a livello di prototipo del quale rimane solo qualche fotografia (1919/20). I documenti fotografici assumono grande importanza visto che il prototipo è andato perduto. Nel tempo esso ha interessato più studiosi e se ne sono tentate diverse ricostruzioni: la più recente nel 1995/96 è stata promossa dalla Fondazione Mazzotta [1] di Milano, in occasione del 75° anniversario della fondazione del Bauhaus, ed attualmente si trova presso le Kunstsammlungen zu Weimar [De Michelis e Kohlmeyer 1996].

Scopo del lavoro è quello di descrivere la forma della Torre del Fuoco attraverso il linguaggio dell'algebra lineare e di darne una ricostruzione virtuale, nella consapevolezza di quanto Itten fosse capace di concretizzare nell'arte il suo forte intuito matematico, pur non potendo formalizzarlo fino in fondo con adeguati strumenti.

JOHANNES ITTEN (1888-1967)
Originario dell'Oberland Bernese, inizia la sua formazione culturale (anche matematica) e artistica a Ginevra, successivamente studia all'Accademia di Stoccarda. Nel 1916 si trasferisce in qualità di insegnante di una scuola d'arte a Vienna, ove è affascinato da circoli culturali in cui si approfondiscono anche tematiche mistiche e religiose. In questo periodo conosce Alma Mahler, vedova del compositore Gustav Mahler e allora moglie di Gropius.

Nel 1919 Gropius lo invita a Weimar per insegnare al Bauhaus: fino al 1923 Itten si rivela docente particolarmente appassionato, assume le funzioni di "maestro della forma" in quasi tutti i laboratori e chiama importanti artisti come Klee e Schlemmer.

Dopo un'aspra rottura con Gropius nel 1923, lavora presso altre scuole d'arte e ne fonda una che avrà alterne vicende a causa della situazione politica tedesca di quel periodo.

Nel 1938 lascia la Germania e ritorna in Svizzera, a Zurigo, dove fino al 1953 dirige la Scuola di Arti Applicate e il relativo Museo. A partire dal 1949 organizza il Museo Rietberg di Arte Contemporanea e ne è direttore fino al 1956. La Kunsthaus di Zurigo, nel 1964, per celebrare l'importanza della sua opera, promuove la prima grande esposizione retrospettiva.

Il progetto della Torre del Fuoco si sviluppa negli ultimi anni del suo soggiorno a Vienna ed il prototipo viene realizzato nei primi mesi della sua attività a Weimar. A quel periodo risale l'importante fotografia del modello della torre illustrato in Figura 1, ripreso di fronte alla Tempelherrenhaus (casa dei Templari), edificio neogotico gia' vagheggiato da Goethe nel suo soggiorno a Weimar e allora atelier di Itten.

GENESI, DESCRIZIONE E MOTIVAZIONE DELLA TORRE
Il progetto della Torre del Fuoco non è marginale nell'opera di Itten: l'importanza della Torre è rilevabile dai numerosi schizzi, dalle dettagliate descrizioni nei suoi Tagebücher (in particolare Tagebuch IX) e dai suoi appunti scritti nel 1964 sul retro di una fotografia del modello.

Anche se in maniera non univoca, se ne deduce la finalità: monumento pubblico quale campanile per una chiesa o faro per l'ampliamento dell'aeroporto di Weimar. Quest'ultima tesi è documentata da una frase dell'autore, "Di notte le pareti di vetro devono essere illuminate dall'interno (come un segnale per gli aviatori!) e superiormente deve essere collocato un faro che ruota" [2], ma non ha avuto riscontro nella realtà, poiché il progetto di ampliamento dell'Aeroporto di Weimar non è mai stato realizzato per mancanza di fondi.

L'opera così particolare è frutto indubbiamente della rielaborazione di idee e di architetture familiari, oltre che dell'evoluzione artistica del tempo. Gli edifici dei paesi vicino a Berna dove Itten ha trascorso parecchi mesi, sia da bambino che in età adulta, l'hanno probabilmente ispirato: l'impianto della struttura interna del castello di Thun, in legno, è costituito da elementi sovrapposti e ruotati rispetto all'asse centrale, così come le scale esterne di alcune case dell'Oberland Bernese spesso suggeriscono un movimento spiraliforme.

Le cataste di legna, che nei paesi delle Alpi Svizzere vengono preparate con sapienti equilibri per la festa nazionale del primo di Agosto e poi a tarda sera bruciate, possono aver suggerito sia la forma che il nome Turm des Feuers.

La formazione matematica dell'autore ha giocato senz'altro un ruolo importante nella scelta degli elementi base compositivi. Nei vari corsi della scuola Bauhaus si lavorava con figure geometriche elementari e loro rielaborazioni, con minore o maggiore razionalità e fantasia. Itten stesso ha scritto in proposito:

Per far vivere agli allievi le forme geometriche elementari in tre dimensioni, feci fare modelli delle forme plastiche quali la sfera, il cilindro, il cono e il cubo [Droste 1994: 28].

Per sottolineare come il quadrato, il cubo, i parallelepipedi siano tra gli elementi geometrici più usati da Itten, dagli allievi e dagli artisti del Bauhaus in genere, si possono citare alcuni lavori eseguiti intorno agli anni venti. L'elenco potrebbe essere assai più ampio, ma è limitato a opere datate nello stesso periodo di ideazione e costruzione del modello della torre.
In tutti i lavori proposti, l'occhio del matematico riconosce, nelle varie rielaborazioni di oggetti geometrici, trasformazioni del piano e dello spazio descrivibili con strumenti dell'algebra lineare:

• Lothar Schreyer - Carte postale (1921) e Wolfgang Molnár - Carte postale (1922) [Droste 1994: 39];
• Rudolf Lutz - Rilievi in gesso con caratteristiche di forme quadrate e rettangolari (1920/21) (Figura 2);
• Else Mögelin - Composizione con cubi (1921) (Figura 3);
• Johannes Itten - Composizione a dadi (Würfel Komposition) (1919) (Figura 4);
• Johannes Itten - Casa dell'uomo bianco (1920) (Figura 5).

L'elenco è chiuso dalla Casa dell'uomo bianco, poichè certamente questa opera ha influenzato molti edifici dell'architettura Bauhaus e soprattutto ha caratterizzato l'evoluzione di indirizzo architettonico sviluppato nella scuola, sotto la direzione di Walter Gropius, a partire dal 1923.

Tra gli edifici sono da ricordare la casa "Am Horn" (Figura 6), ideata da Georg Muche e realizzata (disegni costruttivi ed esecuzione) da Adolf Meyer nel 1923, e le abitazioni dei maestri e degli allievi della nuova scuola Bauhaus aperta a Dessau (1925/26).

Prima di passare alla descrizione matematica del prototipo della torre, sembra significativo citare i numerosi schizzi attraverso i quali il progetto è maturato nel periodo 1919-1920, come appare dai Tagebücher. Molti si riferiscono alla torre stessa, sebbene il motivo della sovrapposizione di cubi, ruotati attorno ad un asse verticale ed eventualmente ridotti, si ripresenti in molti progetti: è utilizzato ad esempio nella realizzazione del campanile di una chiesa [Badura-Triska 1990: II, 330] o è proposto per una variante costruttiva di case (Figura 7).

Anche in significativi ritratti di bambini, risalenti allo stesso periodo, l'autore sembra avere continuamente presente il cubo e le sue trasformazioni. Si rimanda ad un' esempio al Catalogo Mazzotta, ove appare chiaro come il cubo si mescoli prepotentemente ad elementi figurativi [De Michelis e Kohlmeyer 1996: 156].

E' interessante citare anche alcuni commenti che accompagnano i disegni progettuali della torre: essi consentono di precisare dettagli costruttivi e richiamare una simbologia legata a credenze filosofico-religiose dell'artista.

I dodici cubi di cui è composta la torre devono considerarsi raggruppati in tre blocchi. I primi quattro dal basso, previsti di argilla o pietra, sono rispettivamente legati a minerali, piante, animali, uomini. I quattro cubi centrali dovrebbero essere di metallo con inserimento di campane. I quattro cubi superiori, in vetro, rappresentano i quattro elementi (terra, acqua, aria, fuoco) e sopra a tutto deve essere posta una luce gialla (logos-sole).

Il numero dodici non è casuale: in alcuni appunti è stato legato ai dodici segni zodiacali, in altri alle differenti gradazioni dei colori così come sono visibili [De Michelis e Kohlmeyer 1996] in L'uomo nel cerchio dei colori (1919) o in Sfera dei colori in sette gradazioni luminose e dodici tonalità (1921), in altri ancora alle scale musicali (musica dodecafonica).

Nel ricordare che Itten con i suoi studi ha dato un notevole contributo alla teoria dei colori, non va dimenticato che ha affrontato il problema del rapporto tra suono e colore fin dal suo soggiorno a Vienna. L'artista trasferì quindi l'interesse per suoni e colori anche alla scuola di Weimar dove maestri (tra gli altri Gertrud Grunow [BAB 1999]) ed allievi tentarono di dare "un colore " ai suoni.

Nell'opera di Itten la combinazione di forme cubiche è accompagnata da motivi spiraliformi. La spirale, che può essere intesa come simbolo di "ascesa", ha interessato artisti e architetti di ogni tempo: sono soltanto due tra i più noti esempi Brueghel il Vecchio, nel dipinto La torre di Babele, ora nel Kunsthistorisches Museo di Vienna, e il Borromini, con la cupola di S. Ivo alla Sapienza a Roma.

Si vuole evidenziare tuttavia che, quasi fosse una moda del momento, nel passaggio dal XIX al XX secolo molti artisti hanno utilizzato il motivo della spirale per progetti di torri e monumenti. Tra gli altri si ricordano Rodin nel progetto per la torre del lavoro [Ray 1987], Tatlin nel monumento della Terza Internazionale e Obrist ancora per un progetto di monumento [Altamira 1997].

Itten utilizza il motivo della spirale anche nei suoi dipinti: ad esempio in opere famose quali Die Begegnung, 1916 [Badura-Triska 1990: I, 45].[3]

Nei Tagebücher i disegni con motivi a spirale sono spesso accompagnati da studi specifici sul diverso modo di rappresentare tale curva. E' interessante la descrizione di una spirale ottenuta sfruttando il rapporto aureo [Badura-Triska 1990: II, 282].

INTERPRETAZIONE MATEMATICA DELLA TORRE
Gli elementi geometrici che caratterizzano la scultura di Itten sono il quadrato e il cubo, che vengono trasformati per similitudine: ruotati, ridotti (omotetia o scaling), traslati.

Per formalizzare la descrizione di queste trasformazioni risulta particolarmente efficace e sintetico il linguaggio dell'algebra lineare, che sarà applicato prima al piano, per evidenziare la sequenza delle trasformazioni "in pianta", e successivamente allo spazio tridimensionale, per ricostruire la torre "in alzato".

Analisi "in pianta"
Si pensi ora al quadrato di base e ai suoi trasformati, che nel piano rappresentano la proiezione ortogonale dei cubi che compongono la struttura interna della torre: fissato nel piano un sistema di riferimento Oxy, cartesiano ortogonale, si consideri il quadrato di base di lato l, centrato nell'origine e con i lati paralleli agli assi coordinati.

Seguendo la descrizione di Itten, il quadrato è ruotato e ridotto in modo che i vertici di coordinate A₁ (l/2, -l/2), B₁ (l/2, l/2), C₁ (-l/2, l/2), D₁ (-l/2, -l/2) per effetto della roto-omotetia mutino rispettivamente nei punti A₂ (l/2, -l/4), B₂ (l/2, l/4), C₂ (-l/2, l/4), D₂ (-l/2, -l/4) (cfr . il disegno di Itten in Figura 8, Figura 9 e Figura 10).

Utilizzando le tipiche notazioni dell'algebra lineare, vettori colonna a due componenti sostituiscono coppie di coordinate per individuare i punti del piano; dopo la trasformazione i vettori legati ai vertici del quadrato A₁B₁C₁D₁ mutano nei vettori associati ai vertici del quadrato A₂B₂C₂D₂.

La roto-omotetia, che opera la trasformazione così descritta, è composta da una rotazione attorno all'origine O in senso antiorario di un angolo J = arctg1/3 e da una contrazione di fattore k = Ö10/4.

Le due operazioni sono realizzabili attraverso una trasformazione lineare , rappresentabile mediante una matrice M = SR, ove

e .

Nel nostro caso, sostituiti i valori k e J sopra definiti, si ha

.

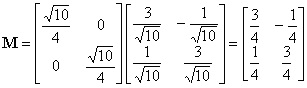Ogni punto del quadrato di partenza di coordinate , ove

,

si trasforma nel punto x' = Mx, ovvero,

=.

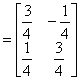
Più in generale, posto x₁=x, applicando successivamente la stessa matrice M ai vettori trasformati, con un processo iterativo si genera una sequenza di quadrati i cui punti sono

, n=1,2,3 … .

Pertanto con la trasformazione L, a partire dal quadrato iniziale, si costruiscono i quadrati di vertici A_nB_nC_nD_n (n= 2 ,… , 12), che insieme ad A₁B₁C₁D₁ rappresentano la proiezione sul piano dei dodici cubi formanti la struttura della torre (cfr. Figura 8 e Figura 9).

Posto l=l₁, sia l_n la lunghezza del lato dell'n-simo quadrato; vale la seguente relazione

, n=1,2, …, 11,

e di conseguenza, 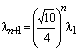.[4]
I segmenti A_n-1A_n, n= 2, 3, …, 12, di lunghezza pari alla quarta parte del lato A_n-1B_n-1, costituiscono una spezzata poligonale S_A. I vertici della S_A appartengono alla spirale logaritmica di equazione vettoriale

,

ove

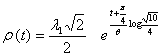, con e J = arctg 1/3.

Si noti che a partire dai vertici B₁C₁D₁ del quadrato iniziale si costruiscono altre tre spezzate poligonali, analoghe alla S_A. Le spezzate S_A , S_B , S_C , S_D sono ottenibili l'una dall'altra con una rotazione, attorno all'origine, di ampiezza p/2 o suoi multipli (lo stesso si può dire delle relative spirali, Figura 10).

Al crescere di n, o per , la lunghezze del lato e allo stesso tempo .

Tenuto conto che la torre ha come basamento due parallelepipedi, sovrapposti e ruotati a loro volta, (cfr. Figura 1), si fa notare che le spirali (o meglio un loro opportuno prolungamento) raccordano anche i vertici delle proiezioni dei rispettivi quadrati di base. Questi ultimi sono legati ai quadrati di proiezione dei cubi della stessa trasformazione lineare L.

Analisi dell'alzato della torre
Il processo iterativo che ha generato i quadrati di base è riconoscibile anche nella descrizione tridimensionale. Infatti, trascurando per ora il basamento della torre e le parti di superfici coniche che completano l'opera, i dodici elementi cubici sovrapposti, indicati nel seguito con K_n, n= 1,2, …, 12, sono ottenuti l'uno dall'altro mediante una roto-omotetia unita ad una traslazione, cioè attraverso una trasformazione affine.

Per una descrizione adeguata di tale trasformazione conviene utilizzare le coordinate omogenee; pertanto ai punti dello spazio tridimensionale si associa il vettore v = [x, y, z, u]_T .
Di conseguenza il cubo K₁, appoggiato sul piano xy, con gli spigoli paralleli agli assi e con il centro del quadrato di base coincidente con l'origine O del riferimento, può essere così descritto (senza ledere generalità, trattandosi di punti al finito, si pone u=1):

.

K₁ viene ruotato in senso antiorario dell'angolo J = arctg 1/3 attorno all'asse z , contratto di un fattore k=Ö10/4 e traslato nella direzione positiva dell'asse z di una quantità pari a l₁ per effetto della affinità rappresentata dalla matrice

,

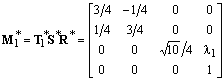essendo R*, S*, T₁^* le corrispondenti matrici di rotazione, scaling e traslazione

.

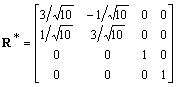
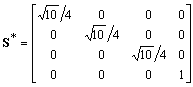
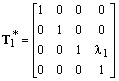I punti v di K₁ vengono trasformati nei punti di K₂, cioè

= .

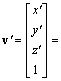
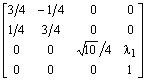
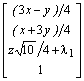I cubi K_n della torre sono generati, uno sull'altro, applicando successivamente la matrice , o equivalentemente applicando ai punti di K₁ le matrici , (n = 1,2, … , 11).

L'altezza h della parte di torre formata dai soli dodici cubi, è ottenuta come somma dei primi dodici termini della progressione geometrica con elemento iniziale l₁ e di ragione Ö10/4, ossia

.

I vertici A_nB_nC_nD_n del quadrato di base inferiore dei cubi K_n appartengono a quattro spirali coniche che si sviluppano sul cono di equazione (in coordinate omogenee (x, y, z, u)

.

Tale cono circolare retto di vertice in V(0,0, al₁, 1) ha come direttrice la circonferenza del piano xy con centro nell'origine del riferimento e raggio ; al₁ rappresenta l'altezza della figura ottenuta dalla sovrapposizione di infiniti cubetti del tipo K_n, quindi

,

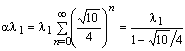da cui a=(8+2Ö10)/3.

Di conseguenza l'equazione vettoriale dell'arco di spirale G_A passante per i punti A_n è:

=,

con .

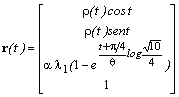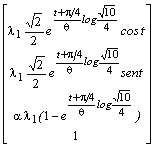Naturalmente da ogni altra sequenza di vertici, B_n , C_n , D_n passano altri tre archi di spirale G_B , G_C , G_D, ottenuti da G_A per successive rotazioni attorno all'asse z, di ampiezza p/2 (Figura 11).

Si osservi che per , le spirali convergono in un unico punto, che è il vertice V del cono e che la loro proiezione sul piano xy viene a coincidere con le spirali piane di Figura 10.

Osservando la fotografia della torre si possono evidenziare altre spirali (o più precisamente spezzate poligonali i cui vertici appartengono a spirali); in particolare risultano evidenti quelle che derivano dall'aggiunta delle componenti decorative di vetro, la cui descrizione si trova al paragrafo successivo.

Basamento e applicazioni laterali in vetro
La ricostruzione della torre si completa con i due basamenti, che non sono cubici, e con le porzioni di superfici coniche, che si innestano su vertici e spigoli delle facce dei singoli cubi.

Basamento. I due basamenti sono parallelepipedi a base quadrata: la legge che fornisce la lunghezza l₀ e l_-1 dei lati dei rispettivi quadrati di base è la stessa omotetia che lega gli spigoli dei cubi K_n, mentre per quanto riguarda le altezze ci sono due diverse costanti di riduzione, una per ciascun basamento.
A partire dal cubo K₁ si può generare il basamento P₀, su cui K₁ è appoggiato, trasformando K₁ mediante la matrice

ove (R*)^-1 è l'inversa della matrice di rotazione R* introdotta al paragrafo precedente e

, .

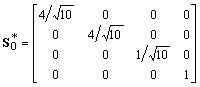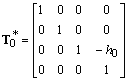Si è scelta l'altezza h₀ = l₀/4 = l₁/Ö10 a seguito di un rilevamento sulla fotografia di Figura1 e in accordo con la ricostruzione promossa dalla Fondazione Mazzotta.

In maniera analoga, modificando opportunamente , si genera il basamento inferiore P_-1 di altezza h_-1. Dallo stesso rilevamento sulla fotografia è presumibile che le due altezze h₀, h_-1 siano in rapporto 7 a 6.

Con h₀ = l₁/Ö10 e h_-1 = 6/7 h₀, si può stimare l'altezza complessiva della torre in funzione del lato l₁ del primo cubo e capire quale sia stata la scelta dell'autore per ottenere un prototipo di circa 3.60 metri di altezza.

L'altezza della ricostruzione virtuale,

induce a supporre che sia stato .

Applicazioni laterali in vetro. Si fa notare che le porzioni di superfici coniche di completamento sono di due tipi:

• le quattro che si innestano sulle facce laterali del cubo K₁, fissate con tiranti al primo basamento, ottenibili l'una dall'altra con rotazioni attorno all'asse verticale;
• le altre che decorano le facce dei cubi superiori, da K₂ in poi, ottenibili su cubi diversi l'una dall'altra con la stessa legge che ha generato la sequenza K_n.

Cercando di essere fedeli al prototipo, i coni legati a K₁ sono stati pensati con vertici sugli spigoli verticali del cubo stesso e aventi come direttrici opportuni archi di ellisse.

Le rimanenti porzioni coniche hanno invece un'indubbia collocazione del vertice, mentre la direttrice, ancora un arco di ellisse, è stata supposta appartenente ad un adeguato piano passante per uno spigolo del cubo.

Gli elementi della ricostruzione virtuale della torre sono proposti in Figura 12.

NOTE
[1] Fondazione Antonio Mazzotta - Foro Buonaparte, 52 - 20121 Milano. ritornare al testo

[2] In der nacht sollten die Glaswände von innen erleuchtet (als Merkzeichen einer Stadt für Flieger!)...Zuoberst wäre ein Leuchtfeuer, das sich dreht [Bogner 1994: 87]. ritornare al testo

[3] Consulta anche il sito Internet ArchitetturaModerna.com. ritornare al testo

[4] Si fa notare che in De Michelis e Kohlmeyer [1996] il rapporto k di riduzione dei lati è erroneamente indicato come 1/3, perché confuso con la quantità r = 1/3, che rappresenta il rapporto tra le parti in cui viene suddiviso il lato stesso per effetto della roto-omotetia.
Dagli schizzi riportati nei Tagebücher si comprende come Itten abbia cercato diverse soluzioni per generare la torre; nel disegno di Figura 8, in basso a sinistra, compare uno studio in cui il rapporto è r =1 e di conseguenza k = Ö2/2.
Inoltre, per la ricostruzione della torre realizzata nel 1971 [cfr. De Michelis e Kohlmeyer] per la Kunsthalle di Norimberga è stato scelto r=1/2 che corrisponde a k=Ö5/3. ritornare al testo

BIBLIOGRAFIA
Altamira, A. 1997. Il Secolo Sconosciuto. Milan: Rossellabigi Editori.

Badura-Triska, E., ed. 1990. Johannes Itten -Tagebücher. 2 vols. Vienna.
Bauhaus Archive Berlin. 1999. Berlin.

Bogner, D., ed. 1994-5. Das frühe Bauhaus und Johannes Itten. Weimar-Berlin-Bern.

Cook, T.A. 1979. The Curves of Life. New York: Dover Publications.

De Michelis M. and A.Kohlmeyer (a cura di). 1996. 1919-1933 Bauhaus. Milan: Fondazione Mazzotta.

Droste, M. 1994. Bauhaus. Berlin: Benedikt Taschen Verlag.

Ghyka, M. 1977. The Geometry of Art and Life. New York: Dover Publications.

Itten, J. 1921. Analyses of Old Masters. In Utopia: Documents of Reality, Bruno Adler, ed. Weimar: Utopia Press.

Manara, C.F. 1967. Lezioni di Geometria. Milano: Edizioni Viscontea.

Ray, S. 1987. L'Architettura dell'Occidente. Rome: La Nuova Italia Scientifica.

RELATED SITES ON THE WWW

Johannes Itten
ModernArchitecture.com: Johannes Itten
Biography of Johannes Itten (in German)

The Bauhaus
Bauhaus: The New Man, the New Technique

GLI AUTORI
Elena Marchetti received her doctorate in mathematics at the Faculty of Sciences at the Università degli Studi di Milano. She was a researcher of mathematical analysis at the Department of Mathematics of the Politecnico di Milano, and since 1988 is an associate professor of "Istituzioni di Matematica" at the Faculty of Architecture of the Politecnico di Milano. For many years she taught in courses of mathematical analysis to engineering students, and since 1988 she teaches mathematics courses to architecture students. Her research activity is concentrated in the area of numeric analysis, principally regarding numeric integration and its applications. She has produced numerous publications in Italian and international scientific journals. Her participation and collaboration in several conferences dedicated to the application of mathematics to architecture has stimulated her interest in this subject. The experience gained through intense years of teaching courses to architecture students has led her to publish several textbooks, one of which regards lines and surfaces and has a multimedia support package, on the production of which she collaborated.

Luisa Rossi Costa diventa Dottore in Scienze Matematica presso l'Università degli Studi di Milano nel Luglio 1970; dopo la laurea frequenta Corsi e Seminari presso la scuola Normale Superiore di Pisa e l'Istituto di Alta Matematica a Roma. Dall'Ottobre 1970 ad oggi insegna in corsi di Analisi Matematica rivolti agli studenti delle Facoltà di Ingegneria del Politecnico di Milano, dove è Professore Associato di Analisi Matematica.
I suoi primi interessi di ricerca si collocano nel Calcolo Numerico su problemi variazionali e sulla determinazione di autovalori complessi. Successivamente nell'ambito dell'Analisi Funzionale, si occupa di problemi legati ad equazioni differenziali a derivate parziali di tipo parabolico e di problemi inversi mirati alla determinazione di superfici di separazione di mezzi con caratteristiche diverse, di coefficienti nell'equazione del calore e di una metrica in geofisica, allo scopo di trovare soluzioni stabili in adeguati spazi funzionali. I risultati ottenuti sono stati oggetti di pubblicazione.
Ha partecipato alla preparazione di lezioni rivolte a studenti del corso di laurea on line di Ingegneria Informatica (laurea triennale). Si occupa inoltre di problemi connessi con la didattica e di orientamento e formazione di studenti delle Scuole Medie Superiori.
Coltivando un costante interesse verso l'Architettura e l'Arte, convinta che la Matematica contenga una forte componente estetica, cerca di sottolineare collegamenti tra questi campi apparentemente molto differenti.

Copyright ©2002 Kim Williams