Versione italiana

Movement gives birth to form, form gives birth to movement. Every point, every line, plane, every body, every shadow, every light, every colour, are forms born of movement, which again give birth to movement. [J.Itten 1921]

INTRODUCTION
The "Bauhaus" artistic movement, which takes its name from the school founded by Walter Gropius in 1919, certainly occupies a very prominent position among the twentieth century currents aiming at a union between art and rationality. The artists who founded it or subsequently took part in it never neglected to juxtapose technical subjects with their artistic studies. Mathematics and geometry generally had a fair space in their school curricula and consequently came out in their artefacts at all artistic levels (painting, sculpture, textile manufacture, etc.) so much so that there are many works, where mathematical-geometrical readings can be obtained [De Michelis and Kohlmeyer 1996; Droste 1994; BAB 1999].

An intriguing example of such an approach is the project for The Fire Tower by Johannes Itten, one of the most important exponents of the movement (Figure 1). The project, frequently mentioned in his Tagebücher (Diaries) [Badura-Triska 1990], was realised as a prototype. Unfortunately only a few photographs, dated around 1919-20, are left; the photographs take on great importance, given that the prototype has long since been lost. Since then many researchers have taken an interest in it and have tried different reconstructions: the most recent reconstruction was commissioned by Fondazione Mazzotta [1] of Milan in 1995/1996, on the occasion of the seventy-fifth anniversary of the foundation of the Bauhaus, and is still located at the Kunstsammlungen zu Weimar.

The aim of this paper is to describe the shape of The Fire Tower with the language of linear algebra and give a virtual reconstruction, in order to understand how Itten managed to concretise his strong mathematical intuition in an artistic form, even though he was unable to formalise it entirely with adequate instruments.

JOHANNES ITTEN (1888-1967)
Born in the Canton of Berne, Itten started his cultural, artistic and mathematical formation in Geneva before going on to the Academy of Stuttgart. In 1916 he moved to Vienna to take up a post as art teacher and, fascinated by Viennese cultural circles, he was soon attracted to religious and mystical themes. In that period he also met Alma Mahler, widow of composer Gustav Mahler and at that time married to Gropius. In 1919 Gropius invited him to the Bauhaus school at Weimar, where he proved an impassioned teacher and, on taking over the classes of form, called important artists like Klee and Schlemmer. After a bitter break with Gropius in 1923, he went to work in other art schools and also founded one of his own, which alternated between success and failure because of the increasing difficulties in the political situation in Germany. In 1938 he left Germany and went back to Switzerland, where he was director of Zurich Arts and Crafts School and its Museum until 1953. From 1949 on he also organised the Rietberg Museum for Contemporary Art, where he was director of both until 1956. In 1964 the Zurich Kunsthaus, to celebrate the importance of his work, organised the first retrospective exhibition dedicated to Itten.

The project of The Fire Tower developed in the last years of his stay in Vienna and the prototype was realised in the first months of his activity in Weimar. The photograph of the Tower model that appears in Figure 1 was taken in that period in front of Itten's studio, which was known as Tempelherrenhaus (Templars' house), a neo-Gothic building that had already conceived by Goethe during his stay in Weimar.

GENESIS, DESCRIPTION AND MOTIVATION BEHIND THE FIRE TOWER
The Fire Tower is not at all marginal in Itten's work: its central importance is pointed out in numerous sketches, from the detailed descriptions in his Tagebücher (particularly Tagebuch IX [Badura-Triska 1990]) and his 1964 notes written on the back of the photograph.

The Fire Tower was probably designed to be a public monument, perhaps a bell-tower for a church or a beacon for the expansion of the Weimar Airport. The latter hypothesis is supported by one the author's observations: "During the night the glass walls must be lightened from inside (as a signal for aviators!) and a turning light must be positioned on the top."[2] The project came to nothing, because the plans to enlarge Weimar Airport had to be abandoned for lack of funds.

Such an exceptional project is undoubtedly the result of re-elaborated ideas and familiar architecture, as well as the artistic mood of the period. The buildings of the villages near Berne where Itten spent many months both as a child and adult, gave him his initial inspiration. Thun castle, for example, seems to have been very important, with its timber interior formed of elements laid one on the other around the central axis. A spiral movement is also often reflected in the exterior stairs of quite a few houses in the Swiss Alps. The elegantly constructed wood bonfires lit on the first of August in the Swiss Alps, probably suggested both the shape for the project and the name chosen by Itten, Turm des Feuers.

Itten's mathematical knowledge undoubtedly played an important role in the choice of the basic component of the tower. In the different Bauhaus courses it was quite common for teachers and students to work with elementary geometric figures and their re-elaborations, with more or less rationality and more or less fantasy. Itten's aim was, as he wrote:

To let the students live the elementary geometric figures in three dimensions, I made models of plastic shapes like the sphere, the cylinder, the cone and the cube [Droste 1994: 28].

The following works, mainly from the twenties, underline how the square and the cube are the elements mostly used by Itten, as well as by the students and artists of the Bauhaus. The list could be longer, but it is limited to the works dated in the same period as the ideation and the construction of the tower model. In all these works the mathematician will recognize plane and space transformations in the different re-elaborations of geometric objects, and can describe them with the instruments of linear algebra:

• Lothar Scheyer - Carte Postale (1921) and Wolfgang Molnàr - Carte Postale (1922), [Droste 1994: 39];
• Rudolf Lutz - Plaster reliefs with characteristics of quadratic and rectangular shapes (1920/21) (Figure 2);
• Else Mögelin - Composition with Cubes (1921) (Figure 3);
• Johannes Itten - Composition with Dice (Würfel Komposition) - (1919) (Figure 4);
• Johannes Itten - The White Man's House (1920) (Figure 5).

The White Man's house determined the architectonic evolution of the Bauhaus school under Gropius's direction (post-1923) and its influence can be seen in many Bauhaus-inspired buildings. Among other buildings worth mentioning are the house Am Horn (Figure 6), projected by Georg Muche and realized (plan and execution) by Adolf Meyer in 1923, and the teachers' and students' houses for the new Bauhaus school in Dessau (1925/26).

Before giving a mathematical description of the prototype for the tower, it is significant to remember the numerous sketches of the project made in 1919-1920, as is apparent in the Tagebücher. Many of them concern the tower, even if the motif of the superimposed cubes, turned around a vertical axis and eventually reduced, is repeated in projects for other buildings. It is, used, for example, in the realization of a church bell-tower [Badura-Triska 1990: II, 330], or is proposed for houses (Figure 7). In significant children's portraits of the same period, Itten also keeps in mind the cube and its transformations. In the Mazzotta Catalogue, for example, the cube is shown as underscored as it mixes with figurative elements [De Michelis and Kohlmeyer 1996: 156].

It is also interesting to read the comments accompanying the tower plans, which give precise building details and help reveal the symbolism connected with philosophic-religious beliefs of the artist. The twelve cubes composing the tower are assembled in three groups. The four bottom cubes, designed to be clay or stone, stand for minerals, plants, animals and humans. The central four cubes are described as being made of hollow metal with bells inside but no symbolic interpretation is offered. The upper four glass cubes represent the four elements (earth, water, air, fire) and above them there is supposed to be a yellow light (logos-sun). The number twelve is not coincidental. In some of Itten's notes it is connected to the twelve zodiacal signs, in others to the different graduations of colours as they are visible in The man in the colours circle (1919) or in Sphere of colours in seven bright graduations and twelve tonalities (1921) [De Michelis and Kohlmeyer 1996], in others to the musical scales (dodecaphonic music).

In mentioning the importance of Itten's studies in colour theory, we need to remember that he had been considering the problem of the relation between colour and sound since his stay in Vienna. The artist had also introduced his interest for sounds and colours in the Weimar school, where teachers (including Gertrud Grunow [BAB 1999]) and students tried to give "colour" to sounds.

The combination of cubic shapes is accompanied by spiral forms in Itten's work. The spiral, often intended as a symbol for "ascent", has always intrigued artists and architects. Two examples of the use of the spiral appear in The Tower of Babel by Bruegel the Elder (now in the Kunsthistorisches Museum, Vienna) and in the cupola of S. Ivo alla Sapienza in Rome by Borromini.

The turn-of-the-century fashion of employing the spiral motif in projects for towers and monuments should also be remembered. as for example, in Rodin's Tower of the Work [Ray 1987], Tatlin's Monument of the Third International and Obrist's Project for a Monument [Altamira 1997]. Itten also used the spiral motif in his pictures, in works such as Die Begegnung (1916) [Badura-Triska 1990: I, 45].[3] In the Tagebücher, drawings of spiral motifs are often accompanied by specific studies on different way to represent this curve; of great interest is the description of a spiral obtained by using the golden ratio [Badura-Triska 1990: II, 282].

THE MATHEMATICAL INTERPRETATION OF THE TOWER

The geometric elements characterising Itten's sculpture are the square and the cube, which are transformed by a similitude: rotated, reduced (scaling) and translated. To formalise descriptions of these transformations, the language of linear algebra is particularly synthetic and efficacious.
First linear algebra is applied to the plane, to underline the sequence of the in plan transformations, and then to the three-dimensional space, in order to build the front elevation of the tower.

In plan analysis
Let us consider the square bases and their transformations, which on the plane represent the orthogonal projection of the cubes forming the inner structure of the tower.

Let l be the length of the square side having its centre in O, origin of the orthogonal co-ordinates of the plane Oxy, and sites parallel to the axes.

Following Itten's descriptions, the square is rotated and reduced so that the vertices A₁ (l/2, -l/2), B₁ (l/2, l/2), C₁ (-l/2, l/2), D₁ (-l/2, -l/2) change respectively into A₂ (l/2, -l/4), B₂ (l/2, l/4), C₂ (-l/2, l/4), D₂ (-l/2, -l/4) (see Itten's drawings in Figure 8, Figure 9 and Figure 10).

Introducing the usual notations of linear algebra, column vectors (with two components) give the points of the plane; after the transformation, the vectors corresponding to the vertices A₁B₁C₁D₁ of the first square change into those giving the vertices A₂B₂C₂D₂ of the second square.

The roto-homothety representing these transformations adds the counterclockwise rotation around the origin O of an angle J = arctg 1/3 to a scale (scaling) with factor k = Ö10/4.

The two transformations represented by a linear transformation , are realised by the matrix M=SR, where

e .

In such a way , with k and J defined above, we obtain

.

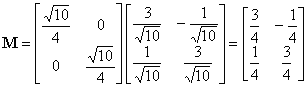Each point of the first square, where

,

changes to x' = Mx, that is,

=.

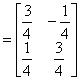
More generally, named x₁=x, the points of the squares generated successively by the transformation L are given as , n=1,2,3… .
The first twelve squares of this sequence are the plane projection of the twelve cubes forming the inside of the tower (see Figure 8 and Figure 9).

Let l=l₁ be the length of the side of the first square and l_n of the n-square with vertices A_nB_nC_nD_n, n=1,2, … , 12.

The relation between them is

, n=1,2, …, 11,

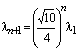that is,.[4]
The segments A_n-1A_n, n = 2,3,…,12 (their length is a quarter of A_n-1B_n-1), form a polygonal line S_A.

The S_A vertices belong to a logarithmic spiral that has the following vectorial equation:

,

where

,

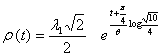with and J = arctg 1/3.

It must be underlined that, starting from the vertices B₁C₁D₁ of the first square, three other polygonal lines S_A S_B S_C S_D are described and, at the same time, other three spirals.

The four polygonals S_A , S_B , S_C , S_D are connected to one other by a rotation of an angle p/2 or mp / 2 (m natural integer), as are the corresponding spirals (see Figure 10).

Increasing n, or for , the length of the side (tends to 0) and at the same time .

The tower has two super-imposed supports with square bases (see Figure 1); these bases are rotated with the same rule, that is the same linear transformation L. It is easy to understand that an adequate extension of the spirals also connects the vertices of the base of the two supports.

Analysis of the front elevation
The iterative process generating the square base is visible in the three-dimensional description.
Let K_n, n = 1,2, …, 12, be the superposed twelve cubes forming the inner part of the tower ( for the moment we exclude the two supports and the parts of conic-surfaces decorating the structure).

The cubes K_n grow one from the other through a roto-homothety and a translation, that is, by means by an affine transformation. The homogeneous co-ordinates are convenient for an adequate description of the affine transformation; therefore a point of the three-dimensional space is represented by a vector v = [x, y, z, y]_T.

In such a way the cube K₁, with one face laying on the plane Oxy, with the edges parallel to the axes and the centre of the base in the origin O, can be described by

.

K₁ is rotated counterclockwise by an angle J = arctg 1/3 around the z-axis, reduced of a factor k=Ö10/4 and translated a quantity l₁ in the positive direction of the z-axis, by the linear transformation represented with the matrix:

,

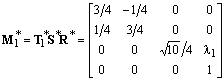where R*, S*, T₁^* are respectively the corresponding matrices of rotation, scaling and translation

.

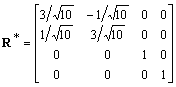
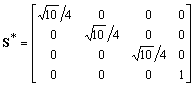
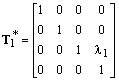The points v of K₁ are transformed in the points belonging to K₂, that is

= .

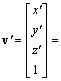
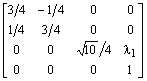
The cubes K_n are generated one on another, applying the matrix successively, or, equivalently, applying to the points of K₁ the matrices , (n = 1,2, …, 11).

The part of the tower formed by the twelve cubes has a height h obtained by adding the first twelve terms of a geometrical progression with the initial element l₁ and factor Ö10/4, that is,

.

Four conic spirals contain the vertices A_nB_nC_nD_n of the inferior base of the cubes K_n and line on the cone written in homogeneous co-ordinate (x, y, z, u) with the following equation:

.

This cone has the vertex in V(0,0, al₁, 1) and the circle section centred in O, with radius , lying on the Oxy plane, as directrix . The value al₁ gives the height of an ideal structure obtained by the superposing infinite cubes K_n,

,

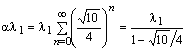that is, a=(8+2Ö10)/3.

The vectorial equation of a spiral line G_A (passing through the points A_n) has the following form

=,

with .

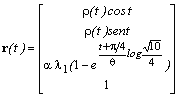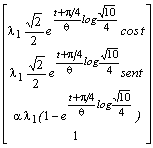Naturally each sequence of the vertices B_n , C_n , D_n, belongs respectively to other three spiral-lines G_B , G_C , G_D, obtained from G_A by rotations around the z-axis of multiples of p / 2 (Figure 11).

It is evident that when , the spirals converge to the same point, the vertex V of the cone, and their projection on the plane Oxy are the spirals represented in Figure 10.

Looking the photograph of the tower, it is possible to pick out other spirals or, more precisely, other polygonal lines having vertices belonging to spirals. Particularly evident are those created from the decorative part of glass described in the following section.

Bases and glass-decorations
The reconstruction of the tower will be concluded with the analysis of the two supports, which are not cubic, and with the portions of conic surfaces, joining vertices and edges of each cube.

Analysis of the base. The two supports are square-based parallelepipeds: the law that furnishes length l₀ and l_-1 of the sides of the respective base-squares is the same homothety that links the vertices of the cubes K_n, while as regards the heights, there are two different constants of reduction, one for each support.
Beginning with cube K₁, the base P₀ on which K₁ is supported can be generated, transforming K₁ by means of the matrix

Where (R*)^-1 is the inverse of the rotation-matrix R* defined in the paragraph above and

, .

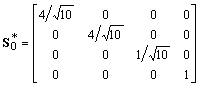The height h₀ = l₀/4 = l₁/Ö10 is deduced from Figure 1, and is in accordance with the reconstruction commissioned by the Mazzotta Foundation.

The inferior support P_-1, with height h_-1, is generated from P₀ following the same process and changing conveniently the matrix . From the examination of the same photograph it is presumed that h₀ and h_-1 are in the ratio 7/6. With h₀ = l₁/Ö10 and h_-1 = 6/7 h₀, it is possible to estimate the height of the entire tower as a function of l₁ and understand the artist's choice for having a model with the height of approximately 3.6 meters.

The height of the virtual reconstruction is

which leads us to the supposition that .
Analysis of the ornament. The ornamental conic portions are of two different kinds:

• the four parts connected with the faces of the cube K₁ and fixed to the first support are obtained one from the other by rotation around the z-axis;
• all the others , which decorate the sides of the superior cubes, starting from K₂, are realised (in different cubes) with the same transformation generating the K_n sequence.

Trying to stick to the model, the cones connected with K₁ are imagined as having the vertex on the vertical edges of the cube, and an adequate arch of ellipses as directrix. All the other conic parts have the indubitable position of the vertices; the arch of ellipse chosen as directrix lies on an adequate plane containing one edge of the cube.

The tower reconstruction modules can be seen in Figure 12.

NOTES
[1] Fondazione Antonio Mazzotta - Foro Buonaparte, 52 - 20121 Milan. return to text

[2] In der nacht sollten die Glaswände von innen erleuchtet (als Merkzeichen einer Stadt für Flieger!)...Zuoberst wäre ein Leuchtfeuer, das sich dreht [Bogner 1994: 87]. return to text

[3] For other examples of Itten's work, see ArchitetturaModerna.com. return to text

[4] It must be underlined that the constant k of reduction of the sides in De Michelis and Kohlmeyer [1996] is erroneously indicated as 1/3, because it was confused with the quantity r=1/3, representing the ratio between the two parts in which the sides are divided after the roto-homothety. Reading the Tagebücher [Badura-Triska 1990] it is evident that Itten looked for different solutions; in the bottom left drawing of fig.8 the ratio is r =1 and consequently k = Ö2/2. The ratio r=1/2 was chosen for the tower reconstruction realised in 1971 for the Kunsthalle of Nürnberg [De Michelis and Kohlmeyer 1996] and this choice corresponds to k=Ö5/3. return to text

REFERENCES
Altamira, A. 1997. Il Secolo Sconosciuto. Milan: Rossellabigi Editori

Badura-Triska, E., ed. 1990. Johannes Itten -Tagebücher. 2 vols. Vienna.

Bauhaus Archive Berlin. 1999. Berlin.

Bogner, D., ed. 1994-5. Das frühe Bauhaus und Johannes Itten. Weimar-Berlin-Bern.

Cook, T.A. 1979. The Curves of Life. New York: Dover Publications.

De Michelis M. and A.Kohlmeyer, eds. 1996. 1919-1933 Bauhaus. Milan: Fondazione Mazzotta.

Droste, M. 1994. Bauhaus. Berlin: Benedikt Taschen Verlag.

Ghyka, M. 1977. The Geometry of Art and Life. New York: Dover Publications.

Itten, J. 1921. "Analyses of Old Masters". In Utopia: Documents of Reality, Bruno Adler, ed. Weimar: Utopia Press.

Manara, C.F. 1967. Lezioni di Geometria. Milan: Edizioni Viscontea.

Ray, S. 1987. L'Architettura dell'Occidente. Rome: La Nuova Italia Scientifica.

RELATED SITES ON THE WWW

Johannes Itten
ModernArchitecture.com: Johannes Itten
Biography of Johannes Itten (in German)

The Bauhaus
Bauhaus: The New Man, the New Technique

ABOUT THE AUTHORS
Elena Marchetti received her doctorate in mathematics at the Faculty of Sciences at the Università degli Studi di Milano. She was a researcher of mathematical analysis at the Department of Mathematics of the Politecnico di Milano, and since 1988 is an associate professor of "Istituzioni di Matematica" at the Faculty of Architecture of the Politecnico di Milano. For many years she taught in courses of mathematical analysis to engineering students, and since 1988 she has taught mathematics courses to architecture students. Her research activity is concentrated in the area of numeric analysis, principally regarding numeric integration and its applications. She has produced numerous publications in Italian and international scientific journals. Her participation and collaboration in several conferences dedicated to the application of mathematics to architecture has stimulated her interest in this subject. The experience gained through intense years of teaching courses to architecture students has led her to publish several textbooks, one of which regards lines and surfaces and has a multimedia support package, on the production of which she collaborated.

Luisa Rossi Costa earned her doctorate in Mathematics in 1970 at Milan University and she attended lectures and courses at Scuola Normale Superiore in Pisa and at Istituto di Alta Matematica in Rome. Since October 1970 she has taught at the Engineering Faculty of the Politecnico of Milan, where she is Associate Professor of Mathematical Analysis. She first developed her research in Numerical Analysis, on variational problems and on calculating complex eigenvalues. Her interest then changed to Functional Analysis and to solving problems connected with partial differential equations of a parabolic type. She also studied inverse problems in order to determinate an unknown surface, an unknown coefficient in the heat equation and a metric in geophysics, with the purpose to find stable solutions in a suitable functional space. She published several papers on these subjects. She took part in the creation of lessons for a first-level degree in Engineering via the Internet. She also researches subjects regarding teaching methods and the formation of high school students. Following a continuing interest in art and architecture, and believing that mathematics contains a strong component of beauty, she tries to connect these apparently different fields.

Copyright ©2002 Kim Williams