

|
Fig. 6. The algebraic properties of the Roman system can be made palpable by considering the equivalent geometric properties based on the interrelation of the proportions: 1, Ö2, and q. For example, if S is either removed or added to SR, this results in RR, as Figure 6a illustrates. This is equivalent to Properties 2 and 3. That 2S +RR = RR is equivalent to Property 1 (see Figure 6b). Finally, if SR is cut in half it forms two SR at a smaller scale (Figure 6c), while two SR added together form an enlarged SR (see Figure 6d) as predicted by Property 4, the doubling property of Table 8. | top of page | back to text | 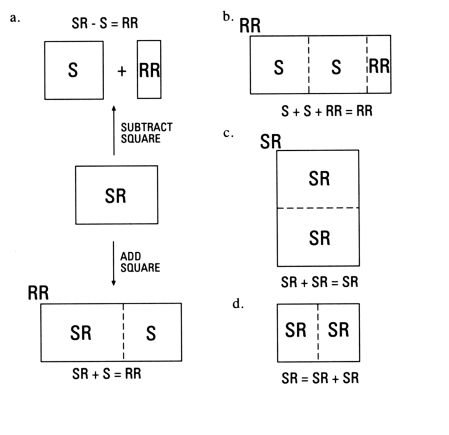
|