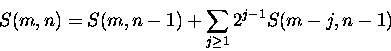 |
(1) |
The terms of the sequence
![]() are known as the small Schröder numbers
(A001003).
Plutarch [13,24]
recorded the numbers 103,049 and 310,952 as being known to Hipparchus
two centuries earlier as counting certain logical propositions.
Recently, as reported in [24], David Hough identified
the first number as the tenth Schröder number, namely
s9
= S(9,9). Habsieger, Kazarian, and Lando [11] have found that
S(9,10) = 310,954 (in our notation),
which differs only slightly from the recorded number of antiquity.
In their explanation, in terms of bracketings counted by
the Schröder numbers, agrees with the straight forward calculation of
S(9,10) from (1).
Subsequently, Sloane [22] has cataloged (as sequence
A010683)
the sequence
are known as the small Schröder numbers
(A001003).
Plutarch [13,24]
recorded the numbers 103,049 and 310,952 as being known to Hipparchus
two centuries earlier as counting certain logical propositions.
Recently, as reported in [24], David Hough identified
the first number as the tenth Schröder number, namely
s9
= S(9,9). Habsieger, Kazarian, and Lando [11] have found that
S(9,10) = 310,954 (in our notation),
which differs only slightly from the recorded number of antiquity.
In their explanation, in terms of bracketings counted by
the Schröder numbers, agrees with the straight forward calculation of
S(9,10) from (1).
Subsequently, Sloane [22] has cataloged (as sequence
A010683)
the sequence
![]() ,
which is the second diagonal of Table 1.a.
,
which is the second diagonal of Table 1.a.
If
s(x) denotes the generating function
![]() ,
then, as one can derive from Lemma 6.1,
s(x) is the combinatorially meaningful solution to
,
then, as one can derive from Lemma 6.1,
s(x) is the combinatorially meaningful solution to
One can associate weighted lattices paths on specific step sets
with the recurrence arrays we consider. The weight of a lattice
path is the product of the weights of its steps, and the weight
of a path set is the sum of the weights of its paths. Let
S[m,n] denote the set of lattice paths from (0,0) to (m,n)that never pass below the line n=m and that use
the infinite set of weighted steps {
(0,1)1, (1,1)1, (2,1)2,
(3,1)4, (4,1)8, ... }. Here the subscripts indicate the step weights.
One can show that S(m,n) is the weight of the paths in
S[m,n]. One can rephrase path weights as
path counts by allowing multiple steps. We remark that
the recurrence
![]() ,
subject to
C(0,0) = 1,
C(m,n) = 0 if m < 0 and
C(m,n)
= 0 if n < m, yields a ``Catalan triangle.''
,
subject to
C(0,0) = 1,
C(m,n) = 0 if m < 0 and
C(m,n)
= 0 if n < m, yields a ``Catalan triangle.''
It is straight forward to show that the array {S(m,n)}
also satisfies the recurrence
The second
triangle
![]() (A033877),
is defined for
(A033877),
is defined for
![]() by the recurrence
by the recurrence
This array is illustrated in Table 1b, with the
sequence
![]() being the large Schröder
numbers
(A006318).
If
being the large Schröder
numbers
(A006318).
If
![]() ,
then, as
one can derive from Lemma 6.1, r(x) is the
combinatorially meaningful solution to
,
then, as
one can derive from Lemma 6.1, r(x) is the
combinatorially meaningful solution to
| x r(x)2 +( x-1)r(x) +1 = 0, | (5) |
One can easily show that
![]() also satisfies the recurrence
also satisfies the recurrence
| R(m,n) = R(m,n-1) + R(m-1, n-1) + R(m-1, n) | (6) |