Chapter 2

Gauss mappings of surfaces

For an embedding X : U -> R³ of a parameter domain U in R² into Euclidean 3-space, the Gauss mapping N : U-> S² sends each point (x, y) of U to the unit normal N = (X_x x X_y) / |X_x x X_y|. The Gauss mapping is singular precisely when 0 = N_x x N_y = K(x, y) X_x x X_y, i.e. on the parabolic set where the Gaussian curvature K(x, y) = 0.

In the terminology of Whitney [Wh] , the Gauss mapping N is good if the gradient of K is never zero on the parabolic set. If N is good, then the parabolic set is a smooth curve (x(t), y(t)). The image N(t) of this curve under the Gauss map is singular precisely when N'(t) = 0. If N is good, then N is excellent if N'(t) = 0 implies N"(t)  0. This ensures that the singularities of the curve N(t) are cusps. Finally, if N is excellent, then N is in general position if the image of N(t) has no triple points or self-tangencies, and no cusp point of N(t) coincides with another image point of N(t).

Whitney proved that a map of surfaces is excellent if and only if its singularities are all equivalent (by smooth changes of coordinates) to folds or cusps. Furthermore, a map of surfaces is stable if and only if it is excellent and in general position. (For a precise definition of stability and a discussion of Whitney's theorem, see [A1] and [GolG].)

We begin our investigation of the singularities of the Gauss mapping with a collection of key examples which exhibit all of the geometric phenomena which we shall associate with these singularities.

Our first three examples are function graphs of the form X(x, y) = (x, y, f(x, y)), so the Gauss map is given by N(x, y) = (-f_x, -f_y, 1)/[(1 + (f_x) ² + (f_y)²]^1/2

We can study the singularities of the Gauss mapping more easily in this case by projecting centrally from the origin to the plane z = 1 to get (-f_x, -f_y, 1). We then project to the xy-plane to get the composed mapping

Ñ(x,y) = (-f_x, -f_y)

Since the image of N is contained in the upper hemisphere, and central projection is a diffeomorphism from the upper hemisphere to the plane z = 1 , the modified Gauss mapping Ñ will have the same singularities as N. In particular N is singular precisely when the Jacobian matrix

has rank less than two, i.e. when the discriminant  = (f_xy)² - f_xx f_yy is zero.

Example 1. The shoe surface:

X(x,y) = (x, y, 1/3 x³ - 1/2 y²)

The modified Gauss mapping is Ñ(x, y) = (-x², y), and the parabolic curve is obtained by solving 0 =  = (f_xy)² - f_xx f_yy = 2 x. Since grad  = (2, 0)  0, the mapping Ñ is good. The parabolic curve can be parametrized by x(t) = 0, y(t) = t. The modified Gauss mapping restricted to the parabolic curve is Ñ(t) = (0, t), with Ñ'(t) = (0, 1)  0, so Ñ is excellent. Thus the Gauss map is stable, with a simple fold along the parabolic curve.

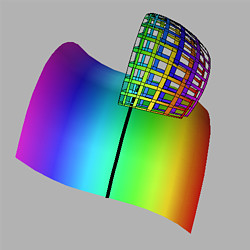
Figure 2.1

The shoe surface and its spherical image.

Example 2. Menn's surface:

X(x, y) = (x, y,  x⁴ + x²y - y²)

Ñ(t) = (2(4  + 1) t³, -3 (4  + 1) t²)

and Ñ'(t) = 0 implies Ñ"(t)  0 , if   -1/4. Therefore the Gauss map is stable if   -1/4, with a cusp at the origin. For  = -1/4, the entire parabolic curve is sent to a single point by the Gauss map. (This is similar to the situation which occurs at the top rim of a torus of revolution -cf. examples 4 and 5 below.) If  < -1/4, f(x, y) =  x⁴ + x²y - y² has an absolute maximum at the origin. If  > -1/4, f(x, y) has a topological saddle point at the origin. The case  = 0 was first studied by Michael Menn.

A related example of a surface with an unstable Gauss map is

X(x, y) = (x, y, 1/4 x⁴ - 1/2 y²)

Ñ(x,y) = (-x³, y)

and  = 3 x², so the parabolic curve is the line x = 0. Since grad  = 6x is zero on the parabolic curve, the Gauss map is not good. Both this surface and Menn's surface occur in the 3-parameter family

X(x, y) = (x, y, a x⁴ + b x²y + c y²)

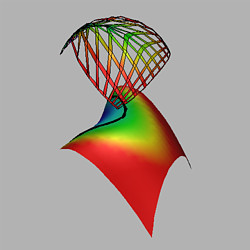
Figure 2.2

Menn's surface and its spherical image ( = -1/2).

Figure 2.3

Menn's surface and its spherical image ( = 1/4).

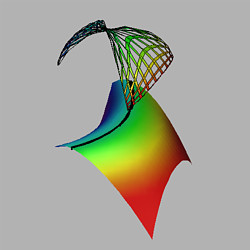
Figure 2.4

Menn's surface and its spherical image ( = -1/4).

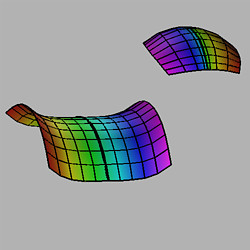
Figure 2.5

The surface z = 1/4 x⁴ - 1/2 y², and its spherical image.