10.45 - 11.45 Uhr

Führung durch das Museum "Reich der Kristalle" (im gleichen Gebäude)

10.45 - 12.00 Uhr im Hörsaal 122:

VideoMath Festival

12.00 - 13.00 Uhr Mittagspause

(für Imbissmöglichkeiten wird gesorgt)

13.00 - 14.30 Uhr in den Hörsälen des Mathematischen Instituts:

Workshops jeweils 45 Minuten:
Ø Gleichungen lösen mit dem TI-92
Ø Erste Schritte in die Analytische Geometrie mit dem TI-92
Ø Fibonacci-Zahlen
Ø Falten eines Hexaflexagons
Ø Origami-Würfel
Ø Magische Figuren
Ø Ist der Mensch symmetrisch?
Ø Geometrie als Spiel
Ø Rallye MatheMatik

Genauere Informationen zu den einzelnen Workshops erhält man durch Anklicken derselben.

14.45 Uhr im Hörsaal 122:

Preisverleihung für die Wettbewerbe und die Rallye

Neben den Hauptpreisen gibt es Trostpreise, unter anderem gestiftet vom Deutschen Museum (100 Karten für freien Eintritt), Carl Hanser Verlag ("Der Zahlenteufel" von Hans Magnus Enzensberger, "Fermats letzter Satz" von Simon Singh), Verlag C. H. Beck ("Pasta all' infinito - meine italienesche Reise in die Mathematik" von Albrecht Beutelspacher), von der Bahlsen GmbH & Co. KG (200 Packungen Leibniz-Keks), von der Alfred Ritter GmbH & Co. KG (50 Tafeln Ritter Sport), vom FC Bayern München e.V. und vom TSV München von 1860 e.V.

Anschließend für Interessierte Rundgang durch das Mathematische Institut, Bibliothek und Rechnerräume. Zum Abschluss bietet sich noch eine Stippvisite in dem im gleichen Gebäude befindlichen, bis 18 Uhr geöffneten Museum "Reich der Kristalle" an (für Teilnehmer am Tag der Mathematik ist der Eintritt kostenlos) - Kristallographie und Mineralogie sind wichtige und interessante Anwendungsgebiete der Mathematik.
 

Programmbeschreibung

"Mathematik ist überall" (Prof. Dr. Dr. h.c. Rudolf Fritsch)

Jedem heute lebenden Menschen ist klar, dass er die Grundrechenarten Addition, Subtraktion, Multiplikation und Division im Alltag ständig braucht, aber er und sie sind sich vielleicht nicht bewusst, dass weit mehr und höhere Mathematik hinter fast allem steckt, womit man im täglichen Leben zu tun hat. Viele Abläufe unseres Lebens beruhen auf der Mathematik, unsere Gesellschaft könnte ohne Mathematik nicht existieren. Das gilt insbesondere für die Technik und die Ingenieurwissenschaften generell, aber auch für die zwischen ihnen und der Mathematik stehende Physik im besonderen. Ebenso können die in unserer Volkswirtschaft und in den Betriebswirtschaften auftretenden Probleme heute nicht mehr ohne grundlegende mathematische Kenntnisse behandelt werden. Die Regelung des Verkehrsflusses in Ballungsräumen und die Computertomographie in der Medizin beruhen auf mathematischen Grundlagen. Die Mathematik ist eine der ältesten Wissenschaften und die Vermittlung mathematischer Fähigkeiten gehört zu den Aufgaben, die sich die Menschheit seit Entwicklung ihres Selbstbewusstseins gestellt hat. Dabei behandelt die Reine Mathematik die Grundlagen, auf denen die verschiedenen Anwendungsfelder aufbauen. Ein Mensch, der wissen will, wo er steht, interessiert sich auch für seine Herkunft, nicht nur die biologische, sondern auch die geistige, in der die Geschichte der Mathematik mit eingeschlossen ist.

"Reich der Kistalle"

durch das Museum führt Dr. Rupert Hochleitner

"VideoMath Festival"

Es handelt sich um eine ausgewählte Sammlung mathematischer Videos, die als Sieger aus einem internationalen Wettbewerb hervorgingen und beim Internationalen Mathematikerkongress 1998 in Berlin vorgestellt wurden. Themen sind unter anderem Probleme in Topologie und Geometrie mit ihren aktuellen Lösungen, Visualisierungen klassischer Ideen von Archimedes, Eratosthenes, Pythagoras und Fibonacci, Mathematik im Gymnasium und Anwendungen moderner numerischer Methoden für Simulation der realen Welt.

Wettbewerbe

Ø Gruppe 1: Jahrgangsstufen 5 und 6

Ø Gruppe 2: Jahrgangsstufen 7 und 8

Ø Gruppe 3: Jahrgangsstufen 9 und 10

Er wird für Teams von jeweils bis zu vier Schülerinnen und Schülern ausgeschrieben. Die Mitglieder eines Teams müssen derselben Gruppe und sollten derselben Schule angehören; sie dürfen jedoch innerhalb einer Gruppe aus verschiedenen Klassen kommen.

Um die ordnungsgemäße Durchführung des Wettbewerbs zu gewährleisten, ist eine Anmeldung mit normaler Post an den

Lehrstuhl für Didaktik der Mathematik
Ludwig-Maximilians-Universität München
Theresienstraße 39
80333 München

didaktik@rz.mathematik.uni-muenchen.de

Jedes Team erabeitet schriftlich Lösungen der gestellten Aufgaben. Deren Themen sind auf die Inhalte des Mathematikunterrichts in den jeweiligen Klassenstufen abgestimmt (siehe die nachfolgenden Beispielaufgaben).

Neben einer gewissen Sicherheit im Rechnen werden vor allem Kombinationsfähigkeit und logisches Denken erwartet.

In jeder Gruppe werden die Teams platziert und die ersten drei Teams mit Preisen bedacht.

Außerdem wird es einen Preis für die beste teilnehmende Schule geben. In diese Bewertung werden jedoch nur Schulen einbezogen, von denen Teams an jeder Gruppe teilgenommen haben. Für jede teilnehmende Schule kommt das beste Team in jeder der drei Gruppen in die Gesamtwertung; der Preis wird der Schule mit der niedrigsten Summe der drei Platzierungen zugesprochen.

Und dann noch etwas. Wie bei allen derartigen Wettbewerben, so gilt auch hier: Der Rechtsweg ist ausgeschlossen.

Die folgenden Aufgaben sollen euch auf den Geschmack bringen, an dem Wettbewerb am Tag der Mathematik teilzunehmen.

Viel Spaß und Erfolg schon bei diesen Aufgaben!

Eine Aufgabe für Gruppe 1 (5. und 6. Jahrgangsstufe):

Hundert Tiere kosten zusammen 100 Euro. Jeder Hund kostet 15 Euro, jede Katze kostet 1 Euro und vier Mäuse kosten zusammen ebenfalls 1 Euro. Wie viele Hunde, wie viele Katzen und wie viele Mäuse sind es?

Eine Aufgabe für Gruppe 2 (7. und 8. Jahrgangsstufe):

Gegeben ist eine Folge von aufeinanderfolgenden ganzen Zahlen, nämlich

1. Wie viele Glieder hat die Folge ?
2. Bestimme (möglichst einfach) den Summenwert aller Glieder der Folge.
3. Bestimme den Produktwert aller Glieder der Folge.
4. Es gibt drei verschiedene Möglichkeiten, drei aufeinanderfolgende Zahlen dieser Folge so auszuwählen, dass ihr Summenwert gleich ihrem Produktwert ist. Wie lauten diese drei Möglichkeiten?
5. Wähle aus der Folge fünf (sieben; neun) aufeinanderfolgende Zahlen so aus, dass der Wert der Summe dieser fünf (sieben; neun) Zahlen gleich dem Wert ihres Produkts ist.

Eine Aufgabe für Gruppe 3 (9. und 10. Jahrgangsstufe):

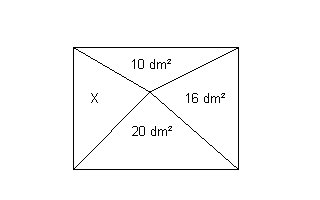Alex hat ein Rechteck in vier Dreiecke unterteilt, von dreien davon den Flächeninhalt angegeben (Dreieck "Oben": A = 10 dm²; Dreieck "Unten": A = 20 dm²; Dreieck "Rechts": A = 16 dm²) und dann gefragt, wie groß der Flächeninhalt des Dreiecks "Links" ist. Welchen Flächeninhalt hat dieses Dreieck?

Informationen zu den Workshops

"Gleichungen lösen mit dem TI-92" (13.00 - 13.45 Uhr)

Nach einer Einführung in die Bedienung des TI-92 werden wir das Thema 'Lösen von Gleichungen' mit geeigneten Experimenten gemeinsam erschließen.

"Erste Schritte in die Analytische Geometrie mit dem TI-92" (13.45 - 14.30 Uhr)

Nach einer Einführung in die Bedienung des TI-92 werden wir erste Schritte in die Analytischen Geometrie tun und Geradengleichungen erkunden (ab der 8. Jahrgangsstufe).

Dr. Gisela Studeny

"Fibonacci-Zahlen" (13.00 - 13.45 Uhr)

Beim Rechnen ist es auch jüngeren Schülern möglich, Entdeckungen an diesen Zahlen zu machen. Interessant ist auch ihr Auftreten in Kunst und Biologie, das wir bastelnd und zeichnend nachvollziehen wollen. (Sofern vorhanden, Taschenrechner mitbringen sowie unbedingt Zirkel und Geodreieck)

Der erste Teil des Workshops, findet von 13.00 bis 13.45 statt und kann für weitere Interessenten in der Zeit von 13.45 -14.30 wiederholt werden. Daneben besteht die Möglichkeit zur Beschäftigung mit Begründungen gewisser Eigenschaften, das ist eher etwas für ältere Schülerinnen und Schüler.

Gisela Pipping, Elisabeth Finckh

"Falten eines Hexaflexagons" (13.00 - 13.45 Uhr)

Ein Flexagon ist ein mathematisches Zaubergebilde. Aus einem Streifen Papier wird eine sechseckige Fläche gefaltet. Diese hat drei Gesichter, von denen zwei zu gleicher Zeit sichtbar sind. Durch geschicktes Drehen zaubert man die verborgene Seite zutage, eine andere lässt man verschwinden.

Konrad Ossiander, Gabriele Söllheim

"Origami-Würfel" (13.00 - 13.45 Uhr und 13.45 - 14.30 Uhr)

Für alle Jahrgangsstufen
Durch geschicktes Falten von farbigen Papierquadraten kann jede(r) mit ein bisschen Geduld und Fingerfertigkeit einen bunten Würfel mit tollem Muster zusammenbauen.
Das Endprodukt darf natürlich mitgenommen werden.

Dr. Renate Motzer

"Magische Figuren" (13.00 - 13.45 Uhr und 13.45 - 14.30 Uhr)

Schon vor Jahrtausenden haben magische Quadrate Menschen in ihren Bann gezogen. Bekannt ist etwa die schon 4000 Jahre alte Geschichte der Schildkröte Lo-Shu aus China, die durch das Zahlenmuster auf ihren Rücken magische Kräfte gehabt haben soll.
In diesem Workshop sollen solche magischen 3*3-Quadrate und andere magische Figuren untersucht werden. Es soll geklärt werden, wie man solch eine Zahlenfigur erzeugen kann und wie viele es davon geben kann.
Der Workshop ist vor allem (aber nicht nur) für Schülerinnen und Schüler der 7. und 8. Klasse gedacht.
Der erste Teil des Workshops, die Einfühung und die Erarbeitung der magischen 3*3-Quadrate findet von 13.00 bis 13.45 statt und kann für weitere Interessenten in der Zeit von 13.45 -14.30 wiederholt werden. Wer sich noch mehr für magische Figuren interessiert, kann sich von 13.45-14.30 auch mit weiteren magischen Figuren vertraut machen.

Gerald Hell

"Ist der Mensch symmetrisch?" (13.00 - 13.45 Uhr und 13.45 - 14.30 Uhr)

In diesem Workshop soll mit Hilfe einer Digitalkamera und einer Computerbearbeitung die Frage nach der Achsensymmetrie des menschlichen Körpers eingehender untersucht werden. Wir erstellen dazu Porträtaufnahmen an verschiedenen Hintergründen und werden diese am Computer spiegeln und über einen Photodrucker ausdrucken.

Verena Schroll

"Geometrie als Spiel" (13.00 - 13.45 Uhr und 13.45 - 14.30 Uhr)

In zwei verschiedenen Spielformen können Schüler und Schülerinnen ihren geometrischen Blick schulen.

• Das Geometriepuzzle erfordert vor allem kombinatorisches Geschick. Es kann allein, zu zweit oder in der Gruppe gespielt werden.
• Tangram als geistiges Kräftemessen zwischen zwei Spielpartnern. Abwechselnd versuchen zwei Spieler/Spielerinnen, ein vorgegebenes Tangram zu legen.

Neben etwas Kombinatorik hilft die Vorstellung von rechtwinkligen Dreiecken verschiedener Größe und deren Flächeninhalten zur raschen Lösung der gestellten Aufgaben. (Für alle Jahrgangsstufen)

Dr. Hella Dietsche, Susanne Kerschl, Petra Leeb

"Rallye MatheMatik" (13.00 - 13.45 Uhr und 13.45 - 14.30 Uhr)

Suche, schätze, rechne! In einer Rallye durch das Mathematische Institut lernst du das Gebäude kennen und erfährst einiges über Ammoniten, berühmte Mathematiker und Hörsäle.

Auch für die Teilnahme an den Workshops ist eine Anmeldung dringend erbeten, damit Räume in der richtigen Größe bereitgestellt werden können.

Die Veranstaltung richtet sich zwar in erster Linie an Schülerinnen und Schüler, selbstverständlich sind aber auch Fachkolleginnen und Fachkollegen willkommen. Zu unserer Information bitten wir um Anmeldung.

Die Veranstaltung wird von folgenden Organisationen unterstützt:

• BMW - Bayerische Motoren Werke AG
• Rektor der Ludwig-Maximilians-Universität München, Prof. Dr. jur. Andreas Heldrich
• Deutsches Museum
• Münchener Rück
• Bayerische Landesbank Girozentrale
• Förderverein Mathematik in Wirtschaft, Universität und Schule an der Ludwig-Maximilians-Universität München
• Texas Instruments
• Carl Hanser Verlag
• Verlag C. H. Beck
• Industrie- und Handelskammer für München und Oberbayern
• Bahlsen GmbH & Co. KG
• Alfred Ritter GmbH & Co. KG
• TSV München von 1860 e.V.
• FC Bayern München e.V.

An der Vorbereitung und Durchführung der Veranstaltung sind folgende Kolleginnen und Kollegen beteiligt:

• StD Manfred Abel, Städtisches Elsa-Brandström-Gymnasium München
• OStRin Helga Borst-Peters, Städtisches Luise-Schroeder-Gymnasium München
• StRin Dr. Hella Dietsche, Carl-Spitzweg-Gymnasium Unterpfaffenhofen
• OStRin Walburga Dirr, Gymnasium Oberhaching
• StDin Sigrid Dreyer, Städtisches Sophie-Scholl-Gymnasium München
• StRin Elisabeth Finckh, Ludwigsgymnasium München
• Prof. Dr. Dr. h.c. Rudolf Fritsch, Ludwig-Maximilians-Universität München
• StR Gerald Hell, Landgraf-Leuchtenberg-Gymnasium Grafenau
• Konservator Dr. Rupert Hochleitner, Mineralogische Staatssammlung München
• StRin Susanne Kerschl, Gymnasium Wolnzach
• AORin i.R. Dr. Isolde Kinski, Ludwig-Maximilians-Universität München
• StD Manfred Kühnel, Städtisches Luise-Schroeder-Gymnasium München
• Dr. Bernhard Kutzler, ACDCA=Austrian Center vor Didactics of Computer Algebra
• StDin Kitty Laubmeier, Albert-Einstein-Gymnasium München
• StDin Angelika Laumer, Städtisches Elsa-Brandström-Gymnasium München
• StRin Petra Leeb, Pestalozzi-Gymnasium München
• StD Wolfgang Mauer, Städtisches Luisengymnasium München
• StRin Dr. Renate Motzer, Ludwig-Maximilians-Universität München
• StDin Margot Obermeier, Städtisches Lion-Feuchtwanger-Gymnasium München
• StD Konrad Ossiander, Giselagymnasium München
• StDin Gisela Pippig, Ludwigsgymnasium München
• StD Thomas Ritter, Luitpold-Gymnasium München
• StDin Dr. Ulrike Schätz, Städtisches Luisengymnasium München
• cand.rer.nat. Manuela Schmieja, Ludwig-Maximilians-Universität München
• OStRin Verena Schroll, Städtisches St.Anna-Gymnasium
• Dipl.-Ing. Christian Sieder, Ingevost, Ingenieurbüro für Verkehrsuntersuchungen im Orts- und Stadtbereich
• StRin Gabriele Söllheim, Giselagymnasium München
• Dr. Wolfgang Steigemann, Bereichsleiter Zentrale Informations- Kommunikationstechnik der Max-Planck-Gesellschaft
• Birgitt Stein, Ludwig-Maximilians-Universität München
• ADin Dr. Gisela Studeny, Ludwig-Maximilians-Universität München