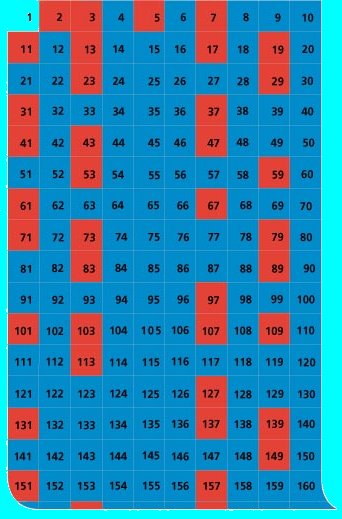
 |
Per
exemple,
(3,5), (5,7), (11,13), (17,19), (29,31), (41,43), (59,61), (71,73),... |
 |
Per
exemple,
(3,5), (5,7), (11,13), (17,19), (29,31), (41,43), (59,61), (71,73),... |

Els
matemàtics creuen que hi ha un nombre infinit de parelles de primers
bessons,
però encara ningú no ha estat capaç de trobar un raonament
que
permeti
assegurar-ho. Amb l'ajut dels ordinadors, s'han anat trobant
parelles
de primers bessons cada cop més grans.
La
parella més gran que es coneix avui dia és:
242206083 x 238880 ± 1
Per a més
informació sobre l'estat actual de les investigacions sobre els
primers bessons
es pot consultar:
http://mathworld.wolfram.com/TwinPrimes.html
Hi
ha nombroses propietats dels nombres primers que són molt senzilles
d'intuir
perquè som capaços de comprovar que són certes per
a llistes
enormes
de nombres. No obstant, no podem estar segurs de que són
certes
per a TOTS els
nombres, perquè no som capaços de provar-les amb
arguments.
No som capaços de trobar una DEMOSTRACIÓ
que ens asseguri la
certesa
del que intuïm, d'una manera irrefutable.
A l'adreça:
http://www.utm.edu/research/primes/
es poden trobar
nombrosos exemples d'aquest fenomen.
Una
d'aquestes qüestions obertes ha arribat recentment als mass-media
de
la mà d'una operació comercial.
L'editor
Tony Faber, amb motiu del llançament del llibre
"L'oncle
Petros i la conjectura de Goldbach",
de
l'autor grec Apostolos Doxiadis, ha ofert un premi de
1
MILIÓ DE DÒLARS a la persona que, abans de dos anys,
sigui
capaç de trobar una demostració del problema anomenat:
CONJECTURA
DE GOLDBACH.
Aquest
problema te el seu origen en una carta que Goldbach adreçà
a Euler
el
7 de juny de 1742, demanant la seva opinió sobre una observació
numèrica:
sembla
que, fora del nombre 2,
TOT
NOMBRE PARELL ÉS SUMA DE DOS NOMBRES PRIMERS.
Euler
contestà a Goldbach que aquest fet semblava d'una certesa
inqüestionable,
però confessà que era incapaç de trobar-ne una demostració.
Els
darrers 258 anys tampoc ningú no ha estat capaç de trobar
un raonament
que
asseguri la validesa d'aquesta afirmació.
Amb
l'ajut dels ordinadors s'ha comprovat la
conjectura
per a tots els nombres parells fins a
4
x 1014
Més informació sobre la conjectura de Goldbach a:
http://www.utm.edu/research/primes/glossary/GoldbachConjecture.html
Text: Enric Nart