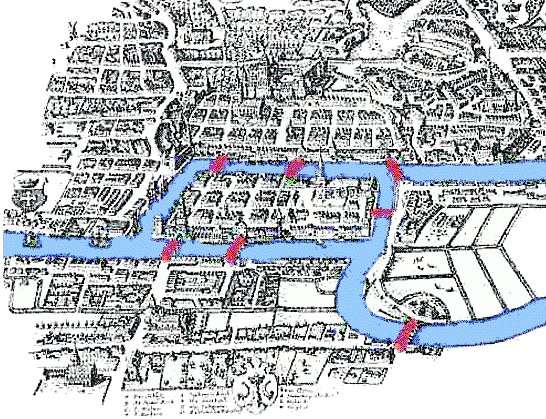
| Tot començà amb les
passejades dels habitants de la ciutat de Königsberg pels ponts sobre
el riu Pregel.
Volien trobar un recorregut que passes per tots i cadascun dels ponts una única vegada i acabés al mateix lloc on havien començat. |
 |
Aquest
és el problema més antic i més conegut de la teoria
de grafs.
| Tot començà amb les
passejades dels habitants de la ciutat de Königsberg pels ponts sobre
el riu Pregel.
Volien trobar un recorregut que passes per tots i cadascun dels ponts una única vegada i acabés al mateix lloc on havien començat. |
 |
Però
els seus intents eren en va.
No hi havia manera de trobar un recorregut amb aquestes condicions.
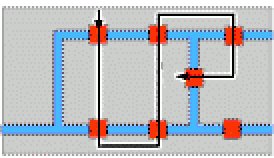 Així, no...
Així, no... |
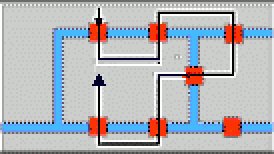 I així, tampoc!
I així, tampoc! |
El
1736, L. Euler publicà un treball, que es considera el primer en
teoria de grafs, en el que investigà el problema dels ponts en termes
matemàtics.
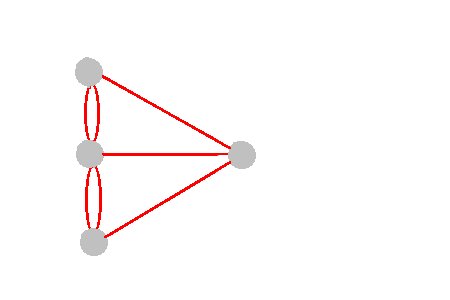
| Per resoldre
el problema, Euler va representar cada tros de terra per un punt i cada
pont per una línia que uneix els punts corresponents.
Així obtingué una representació esquemàtica com aquesta |
 |
Generalitzant
aquesta idea, arribà a la noció de graf.
Amb elements tan simples com són els punts i les línies entre
ells, els anomenats vèrtexs
i arestes
del
graf, hom pot fer models esquemàtics de situacions ben diverses
i estudiar-les matemàticament.
Euler generalitzà el problema inicial i obtingué un criteri per reconèixer quan qualsevol graf es pot recórrer amb un camí tancat, passant una única vegada per cadascuna de les arestes.
El nombre d'arestes incidents en un vèrtex s'anomena el seu grau.
El criteri que donà Euler només es fixa en la connexió
del graf (hem de poder anar d'un vèrtex a qualsevol altre per les
arestes) i en els graus dels vèrtexs: "Han
de ser tots de grau parell"
| Per tant, com que tots els vèrtexs són de grau senar, el problema dels ponts de Königsberg no té solució. No existeix cap recorregut amb les propietats desitjades | 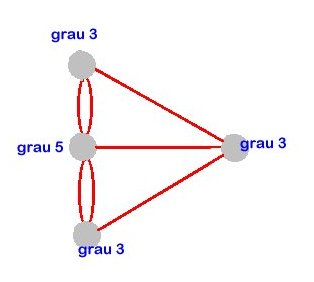 |
 |
 |
 |
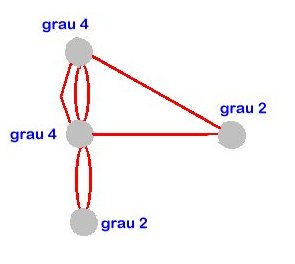
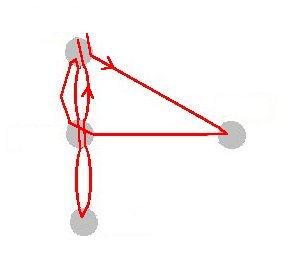
| Però un graf com aquest, amb tots els vèrtexs de grau parell, sí que admet un recorregut com el que volem. | Per exemple, aquest. | Que, interpretat en el context original, correspon a aquest recorregut. |
Si vols més informació la pots trobar a