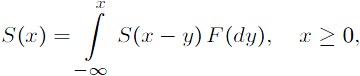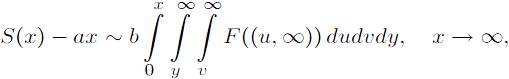Том
51 (2010), Номер 6, с. 1430-1434
Сгибнев М. С.
Асимптотическое свойство решения однородного обобщенного уравнения Винера — ХопфаРассматривается однородное обобщенное уравнение Винера — Хопфа
где F — распределение вероятностей в
где a и b — положительные константы, выражаемые в явном виде.с нулевым средним, конечной дисперсией и бесконечным моментом
x3F(dy). Его P*-решение S(x) обладает свойством
Sgibnev M. S.
An asymptotic property of the solution to the homogeneous generalized Wiener-Hopf equationWe consider the homogeneous generalized Wiener-Hopf equation
wehere F is a probability distribution on
where a and b are explicit positive constants.with zero mean, finite variance, and infinite moment
x3F(dy). Its P*-solution S(x) enjoys the property
Полный текст статьи / Full texts:
![]()