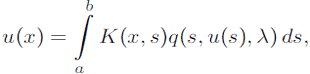Сидоров Н. А., Сидоров Д. Н.
О решении интегрального уравнения Гаммерштейна в нерегулярном случае методом последовательных приближенийВетви решения нелинейного интегрального уравнения
где— параметр, строятся методом последовательных приближений. Рассмотрен случай, когда единица является
характеристическим числом ядра K(x, s) ранга n ≥ 1, точка λ = 0 является точкой ветвления решения. Главный член построенной в работе асимптотики используется как начальное приближение. Равномерная сходимость метода в окрестности точки ветвления устанавливается с помощью теоремы о неявном операторе и леммы Шмидта.
Sidorov N. A., Sidorov D. N.
Solving the hammerstein integral equation in the irregular case by successive approximationsThe branches of a solution of the nonlinear integral equation
whereis a parameter, are constructed by successive approximations. Under consideration is the case when unity is a characteristic number of the kernel K(x, s) of rank n ≥ 1, and λ = 0 is a bifurcation point. The principal term of the asymptotic expansion constructed is used as an initial approximation. The uniform convergence is established in some neighborhood about the bifurcation point on using the implicit function theorem and the Schmidt lemma.
Полный текст статьи / Full texts:
- PDF file (435 KB)
- PostScript file (790 KB)
![]()
Адрес редакции:
пр. Коптюга, 4,
Новосибирск 630090.
Телефон: (383-2) 333-493
E-mail: smz@math.nsc.ru