Судоплатов С. В. 
Об обогащениях и расширениях властных орграфов

Исследуется проблема обогащения и расширения структуры стабильного властного орграфа до структуры стабильной эренфойхтовой теории. Определяются понятия типовой нестабильности и типового свойства строгого порядка. Устанавливается наличие типового свойства строгого порядка у любой бесконтурной графовой структуры с бесконечной цепью. Доказывается, что простейший вид обогащения властного орграфа до структуры эренфойхтовой теории — обогащение 1-несущественной упорядоченной раскраской и локально графово -определимыми многоместными отношениями, позволяющими взаимно реализовывать неглавные типы, — не способен сохранить структуру в классе стабильных структур и, более того, в силу типового свойства строгого порядка порождает формульное свойство строгого порядка. Определяется понятие локально счетно категоричной теории (LCC-теории) и доказывается, что если p₁(x), … , p_n(x) — все неглавные 1-типы данной LCC-теории, то подчинение типу q всех типов r(x₁, . . . 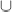, x_m), содержащих (x₁) … (x_m), влечет властность типа q.

Sudoplatov S. V.
On expansions and extensions of powerful digraphs

We study the problem of expanding and extending the structure of a stable powerful digraph to the structure of a stable Ehrenfeucht theory. We define the concepts of type unstability and type strict order property. We establish the presence of the type strict order property for every acyclic graph structure with an infinite chain. The simplest form of expansion of a powerful digraph to the structure of an Ehrenfeucht theory is the expansion with a 1-inessential ordered coloring and locally graph -definable many-placed relations, which enable us to mutually realize nonprincipal types; we prove that this expansion is incapable of keeping the structure in the class of stable structures, and moreover, by the type strict order property it generates the first-order definable strict order property. We define the concept of a locally countably categorical theory (LCC theory) and prove that given the list p₁(x), … , p_n(x) of all nonprincipal 1-types in an LCC theory, if all types r(x₁, . . . 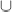, x_m) containing (x₁) … (x_m) are dominated by some type q then q is a powerful type.

Полный текст статьи / Full texts:

• PDF file (415 KB)
• PostScript file (765 KB)