Surveys in Mathematics and its Applications

ISSN 1842-6298
 Volume 1 (2006), 111 - 116

EXISTENCE OF POSITIVE SOLUTION TO A QUASILINEAR ELLIPTIC PROBLEM IN RN

Dragoş-Pătru Covei

Abstract. In this paper we prove the existence of positive solution for the following quasilinear problem

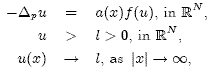
where is the p-Laplacian operator.
The proof is based on the results due to Diaz-Saa ([2]).

2000 Mathematics Subject Classification: 35J60.
Keywords: quasilinear elliptic problem, p-Laplacian, positive solution.

Full text

References

  1. K. Chaib, A. Bechah and F. De Thelin, Existence and uniqueness of positives solution for subhomogeneous elliptic problems in RN. Revista de Mathematicas aplicadas, 21 (1-2) (2000), 1-18. MR1822068(2001m:35099). Zbl 0982.35038.

  2. J. I. Diaz and J. E. Saa, Existence et unicite de solutions positives pour certaines equations elliptiques quasilineaires, CRAS 305 Serie I (1987), 521-524. MR0916325(89e:35051). Zbl 0656.35039.

  3. E. DiBenedetto, $C^{1,\alpha}$- local regularity of weak solutions of degenerate elliptic equations, Nonlinear Anal. 7 (1983), 827-850. MR0709038(85d:35037). Zbl 0539.35027.

  4. J. V. Goncalves and C. A. Santos, Positive solutions for a class of quasilinear singular equations, Electronic Journal of Differential Equations, Vol. 2004 No. 56, (2004), 1-15. MR2047412(2004m:34065). Zbl pre02100297.

  5. G. M. Lieberman, Boundary regularity for solutions of degenerate elliptic equations, Nonlinear Anal. 12 (11) (1988), 1203-1219. MR0969499(90a:35098). Zbl 0675.35042.

  6. N. Ural'tseva, Degenerate quasilinear elliptic systems, Zap. Naucn. Sem. Leningrad. Otdel. Mat. Inst. Steklov 7 (1968), 184-222. Zbl 0199.42502.

  7. J. L. Vazquez, A strong maximum principle for some quasilinear elliptic equations, Appl. Math. Optim. 12 (1984), 191-202. {MR0768629(86m:35018). Zbl 0561.35003.

  8. Z. Zhang, A remark on the existence of entire solutions of a singular semilinear elliptic problem, J. Math. Anal. Appl. 215 (1997), 579-582. MR1490771(98j:35055). Zbl 0891.35042.

Acknowledgement. This work was supported by the CEEX grant ET65/2005, contract no 2987/11.10.2005, from the Romanian Ministry of Education and Research.

Dragoş-Pătru Covei
University Constantin Brâncuşi of Târgu-Jiu,
Bld. Republicii 1, 210152, Târgu-Jiu,
Romania.
e-mail: dragoscovei@utgjiu.ro
http://www.utgjiu.ro/math/dcovei/

http://www.utgjiu.ro/math/sma