There is a great deal of literature that revolves around the manipulation of the square through the geometrical processes of ad quadratum, the 'sacred cut,' and the 'golden rectangle'. They have been the topics of discussion at previous Nexus meetings. The processes that lead to the production of ad quadratum, the golden rectangle, and the sacred cut exploit the properties of the square, but they do so only by virtue of the existence of a primal figure, a first and original square, to operate on and make the subsequent exploitation of its properties possible. That 'first' square has to be the result of a simple, clear, effective and efficient method of construction: a method that constituted its original geometry and established its perfection as the instrument for all subsequent geometrical and metrological manipulations.

The paper deals directly with this puzzle of the first square, tracing its origins to the emergence of the western architectural tradition in ancient Egypt. The question that it will ask and answer is : "how did that original square - that first figure we manipulate in and through these geometrical processes - get there in the first place?" It will do this by showing that there are recurring references to a very specific pair of measures in the history of the architect's practices, and that there are recurring discussions of techniques for their application.

Stretching the Cord: An Egyptian geometer checking the right angle on a block of stone. Ippolito Rosellini, Monumenti Civile, Pisa, 1834.

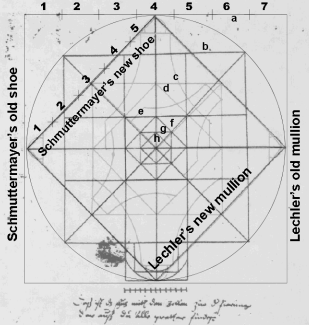
Those references occur in the Roman period in the texts of Vitruvius and Faventius, in the early and late medieval texts by de Honnecourt, Roriczer, Schmuttermayer and Lechler, and in the Renaissance works of Alberti, Serlio and Palladio among others. Lorenz Lechler calls these measures the 'old' and the 'young' shoes, and makes the point that the young is always "taken out of the old." He also makes the point that these measures were established by the teachings of the 'old fathers,' and that his tradition held that they originate in ancient Egypt in the time of the first pharaohs.

As one looks at the history of measure in ancient Egypt, one finds references to a 'new' measure that is also taken out of the 'old.' It is called the remen, and it is derived directly from the measure called the great or royal cubit. Its numeric - and therefore mathematical - relationship to the cubit is identical to the close approximation of the 1:Ö2 relationship that Lechler - and de Honnecourt before him - established between his old and new shoes, and that Faventius and Vitruvius establish as the two measures essential to 'composing the square to perfect standards.'

The paper argues that the existence of two common measures in ancient Egypt - the 20 digit remen and the 28 digit cubit - essentially solves in an elegant and convincing way the puzzle of construction of the first square. It suggests that there was a simple, clear, effective and efficient technique using two cords, with one knotted in remen and the other knotted in cubits, that allowed the ancient Egyptian architect to construct that first square from which all subsequent squares and proportions were derived with an amazingly high degree of geometric accuracy. That technique - known to the Ancient Egyptians as 'the stretching of the cord' - had its origin in the time of the old kingdom in ancient Egypt: in the archaic time of Djoser, Imhotep, Snefru, Amenhotep and Kanofer, the 'old fathers,' and the time of the construction of the first great pyramids and the invention of the geometer's - and the architect's - art.

ABOUT THE AUTHOR
Peter Schneider was born and educated in South Africa, where he taught and practiced architecture before moving to the United States in 1977. He has taught architecture and directed graduate and undergraduate architecture programs in Alabama, Louisiana and Colorado. He currently teaches architectural history, theory and design at the Boulder and Denver campuses of the University of Colorado. His scholarly and research interests have been focused on the history of the architect: on the architect's mind, methods and manners as these have occurred in history, and in the way that the interactions between these three forces have shaped the discipline's traditions. He, like Louis Kahn, loves beginnings, and so his particular focus has been on exploring and understanding the forces that shaped the origin of the architectural tradition, and on the persistent influence those original ideas have had in shaping and forming the persona of the architect. His writings on the history of the architect and the architect's methods and practices have been widely published, and he has lectured on the topic extensively. He is currently exploring and writing about the connections that exist between the myths of architecture's archaic origins and the traditions embedded in its first, archetypal artifacts.