
| Architecture and Mathematics Since 1960 |
|---|
How House
2422 Silver Ridge Avenue
Los Angeles CA 90039-3322 USA
This survey of mathematical applications in architectural design since 1960 traces personal experiences in practice and theory, and does not pretend in anyway to cover the whole field.
The introduction of computers has manifestly changed the relationship of mathematics to architecture over the past forty years.
A distinction is made between mathematics which tends towards abstract generalizations, and architecture which is concretely particular. Mathematical physics used in the service of predicting architectural performance in particular instances is set aside, although this is probably the single, most common usage. Instead, the role that mathematical thought plays in furthering generic knowledge of architectural form is given emphasis. In proposing the study of form, Karl Friedrich Froebel identified three categories: quantitative, qualitative and relational. These are used to organize this survey.
Quantitative studies measure the various material dimensions of form: length, area, volume. The quantitative relationships between building forms, heights, areas of sites, road widths, open areas are examined in early "land use and built form studies". The proposal to redevelop the national and government center in Whitehall, London, is cited. The same line of thought is extended to urban forms and questions of urban densities.
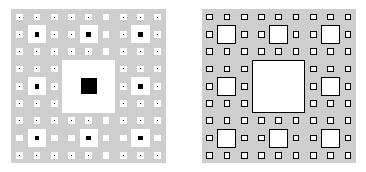
Qualitative studies of form emphasize spatial transformations, the modern group theory of symmetry, and topological relations. Distinct architectural forms may well be equivalent under symmetry, or topology. An example is given of an application of Polya's enumeration theorem.
Relational studies of form were said, by Froebel, to be "forms of life". Whatever their dimensions, or their symmetrical, or topological disposition, the forms now represent a potential design occasion. Advances in shape computation address such relations - especially, in the work of George Stiny and colleagues.
ABOUT THE AUTHOR
On the personal recommendation
of Alan Turing, Lionel
March was admitted to Magdalene College, Cambridge, to
read mathematics under Dennis Babbage. There he gained a first
class degree in mathematics and architecture while taking an
active part in Cambridge theater life. In the early sixties,
he was awarded an Harkness Fellowship of the Commonwealth Fund
at the Joint Center for Urban Studies, Harvard University and
Massachusetts Institute of Technology under the directorships
of Martin Meyerson and James Q Wilson. He returned to Cambridge
and joined Sir Leslie Martin and Sir Colin Buchanan in preparing
a plan for a national and government center for Whitehall. He
was the first Director of the Centre for Land Use and Built Form
Studies, now the Martin Centre for Architectural and Urban Studies,
Cambridge University. As founding Chairman of the Board of the
private computer-aided design company, he and his colleagues
were among the first contributors to the 'Cambridge Phenomenon'
- the dissemination of Cambridge scholarship into high-tech industries.
In 1978, he was awarded the Doctor of Science degree for mathematical
and computational studies related to contemporary architectural
and urban problems.
Before coming to Los Angeles he was Rector and Vice-Provost of
the Royal College of Art, London. During his Rectorship he served
as a Governor of Imperial College of Science and Technology.
He has held full Professorships in Systems Engineering at the
University of Waterloo, Ontario; and in Design Technology at
The Open University, Milton Keynes. At The Open University, as
Chair, he doubled the faculty in Design and established the Centre
for Configurational Studies. He came to UCLA in 1984 as a Professor
in the Graduate School of Architecture and Urban Planning. He
was Chair of Architecture and Urban Design from 1985-91. He is
currently Professor in Design and Computation and a member of
the Center for Medieval and Renaissance Studies. He was a member
of UCLA's Council on Academic Personnel from 1993, and its Chair
for 1995/6. He is a General Editor of Cambridge Architectural
and Urban Studies, and Founding Editor of the journal Planning
and Design. The journal is one of four sections of Environment
and Planning, which stands at "the top of the citation
indexes." Among the books he has authored and edited are:
The Geometry of Environment, Urban Space and Structures,
The Architecture of Form, and R. M. Schindler: Composition
and Construction. His most recent research publications include:
"The smallest interesting world?", "Babbage's
miraculous computation revisited," "Rulebound unruliness,"
"Renaissance mathematics and architectural proportion in
Alberti's De re aedificatoria," and "Architectonics
of proportion: a shape grammatical depiction of classical theory."
His book Architectonics of Humanism: Essays on Number in Architecture
before The First Moderns, a companion volume to Rudolf Wittkower's
Architectural Principles in the Age of Humanism was published,
together with a new edition of the Wittkower, in the Fall 1998.
|
Lionel March, "Architecture and Mathematics Since 1960", pp. 7-33 in Nexus IV: Architecture and Mathematics, eds. Kim Williams and Jose Francisco Rodrigues, Fucecchio (Florence): Kim Williams Books, 2002. http://www.nexusjournal.com/conferences/N2002-March.html |
|
|
|
|
