Evidence of dynamic interaction between geometric research and architectural design can be found in the Roman world, around the beginning of the second century B.C., in late Republican times. In those years a new type of building appears in Roman culture: the amphitheater. It was immediately characterized by a closed elliptic shape that had never been previously adopted in architectural design, and never would be re-used for other purposes in Roman culture.

Architecture and geometry interact when new morphologies appear. Architecture has such qualitative and quantitative demands that it not only brings theoretical geometry into practical application, but also leads it to the establishment of new theories. The creation of a new shape always requires extensions of previous knowledge, as it opens new queries and forces one to work out new diagrams and models.

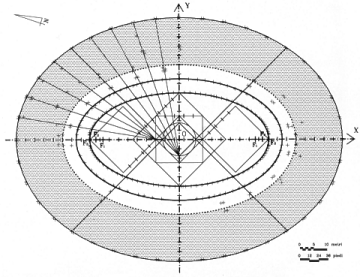
Geometric pattern of Pompeii's amphitheater. In the gray area (ima and summa cavea), the ground was raised above its natural level. In the white part (arena and podium), the level is inferior to the original ground

The end of the third century B.C. corresponds to the acme of the Golden Age of Greek mathematics, whose last heroes were Archimedes, Eratosthenes, Apollonius of Perga, Nicomedes. Archimedes and Apollonius are famous for having devoted much effort to the study of conics and conoids. Thus, the first apparition of elliptic-shaped buildings in southern Italy no earlier than the beginning of the second century B.C. puts us in front of a triple coincidence: historical, geographical and morphologic. We may therefore consider that these simultaneities and similarities are not due to chance, but that the necessity of designing a new building type provided theoretical mathematics with a successful field of direct and immediate experimentation.

Are amphitheaters elliptic or oval? The question has already been widely debated.

In order to understand how the new typological pattern for amphitheaters was first drawn, and how it was transformed into a variety of archetypal models during its historical evolution, inquiries must be made on early samples, buildings that were erected in the late Republic or early Empire. These are much less sophisticated monuments than the late Flavian ones, but they testify to the first attempts to apply a new geometric scheme to architectural design. The measured survey of the amphitheaters of Pompeii (Campania), Roselle (Etruria), and Veleia (Emilia) and the mathematical analysis of their curves evidences three different geometric diagrams deriving from three different answers to the same query.

The design of amphitheaters involves two of the classic problems of ancient mathematics: the quadrature of the circle and the trisection of the angle. The curve of the outer perimeter has to be approximated by an irregular polygon in order to determine the position of the vertices from which the stairs would come down the steps of the cavea, dividing it into cunei of more or less identical size.

Esthetical demands and arithmetic necessities had to converge toward coherent and scientific geometric patterns. One of these would later be called "the perfect oval" by the architects of the Renaissance.

ABOUT THE AUTHOR
Sylvie Duvernoy is an architect, graduated at Paris University in 1982. She later participated in the Ph.D. program of the Architecture School of Florence University and was awarded the Italian degree of "Dottore di Ricerca" in 1998. She presently teaches architectural drawing at the engineering and architecture faculties of Florence University. The researches carried forth since the beginning of the post-graduate studies mainly focus on the reciprocal influences between graphic mathematics and architecture. Architecture history shows that geometry and its related aesthetic symbolism were always present, hidden in architectural and urban design from antiquity to modern times. The way they were involved and the strength with which they were claimed, vary according to historical periods. These relationships have always been expressed by the means of the drawing: the major and unavoidable tool of the design process. The results of her studies were published and communicated in several International Meetings and Reviews.
Beside the research and teaching, she always had a private professional activity. After having worked for a few years in the Parisian office of an international Swiss architecture firm, she is now partner of an associate office in Florence, the design projects of which cover a wide range of design problems, from remodeling and restoration to new constructions, in Italy and abroad.