| The Mathematics Of Palladio's Villas: Workshop '98 |
|---|
Department of Mathematical Sciences
Sweet Briar College
Sweet Briar, VA 24595 USA
 |
The purpose of the workshop was to study the mathematical aspects of the designs of Andrea Palladio's villas in situ with scholars knowledgeable in the relationships between architecture and mathematics (Fig. 1) |
This three-day research tour of eight of Palladio's villas occurred 10-12 June 1998, following the conference Nexus '98: Relationships Between Architecture and Mathematics.[1] The participants of the workshop were:
- Stephen Wassell, author of this paper, director of the 1998 workshop tours of the villas of Palladio.
- Kim Williams, architect and author of Italian Pavements: Patterns in Space, organizer of the Nexus conferences, editor of the online Nexus Network Journal.
- Vera W. de Spinadel, Director of the Centre of Mathematics and Design of the Faculty of Architecture, Design and Urbanism at the University of Buenos Aires, Argentina, co-director of the Mathematics & Design conferences.
- David and Ruth Spieser, the former of whom is Professor Emeritus of the Catholic University of Louvain, Switzerland, as well as an expert on symmetry.
- Rocco Leonardis, architect, artist, and educator based in New York, expert on Italian art and culture.
- Michael Ostwald, Assistant Dean of the Faculty of Architecture at the University of Newcastle, Australia, and director of the architectural theory program there, who joined us for the first day.
- Susan Knight, translator/interpreter and art tour consultant working in Tuscany.
The workshop was a great success, thanks in large part to thorough planning by Kim and Susan. The villas visited during the 1998 workshop were: Villa Pisani Ferri De Lazara, Bagnolo di Lonigo; Villa Rotonda, Vicenza; Villa Valmarana Bressan, Monticello di Conto Otto; Villa Valmarana Malinverni, Lonedo di Lugo; Villa Barbaro, Maser; Villa Emo, Fanzolo; Villa Cornaro, Piombino Dese; Villa Foscari (La Malcontenta), Gambarare di Mira.
The workshop succeeded most immediately in providing the participants with the first-hand experience essential to fully appreciating Palladio's designs. More importantly, in my mind, relationships were formed that has lead to continued discourse and collaboration. The discussions during, between, and after visitations to the villas involved issues crucial to understanding our own reactions to Palladio's work, by allowing us to challenge each other with deliberate, directly motivated queries. Much of the discussion has focused on the underpinnings of beauty, especially concerning the role of proportion, since this has been such a central theme in the literature on Palladio (further discussed below). Are certain proportions inherently more aesthetically pleasing than others are, and if so, why? While discussions of proportions produced as many questions as answers, consensus was reached on Palladio's brilliant use of geometric forms, both in two and three dimensions, and his artful use of symmetry as a consistent design principle (Fig. 2).
 It
was agreed that the sheer variety of designs found in his architecture
is further evidence of his genius. While Palladio certainly used
various aspects of mathematics as design tools, there could be
no mathematical formula that would capture his design process.
Palladio's ability to shape spaces, individually as well as in
combination (which inherently necessitates conceiving designs
in the four dimensions of space-time), and then to articulate
those spaces masterfully using classical forms, is what ultimately
sets his work apart.
It
was agreed that the sheer variety of designs found in his architecture
is further evidence of his genius. While Palladio certainly used
various aspects of mathematics as design tools, there could be
no mathematical formula that would capture his design process.
Palladio's ability to shape spaces, individually as well as in
combination (which inherently necessitates conceiving designs
in the four dimensions of space-time), and then to articulate
those spaces masterfully using classical forms, is what ultimately
sets his work apart.
The discussions during the workshop, and the collaborations that have developed since, center chiefly on the issue of proportion in Palladio's architecture. To best understand the goals of a future workshop, it is necessary to review the rich literature concerning one of the most influential architects of the Renaissance. This thread of research was started, in this century at least, by Rudolf Wittkower, author of Architectural Principles in the Age of Humanism. In this 1949 classic Wittkower makes a strong case that Renaissance architects such as Alberti and Palladio used proportions derived from music in their architecture; because such "harmonic proportions" are beautiful to the ear it was belived they were part of a higher universal design, and thus equally beautiful to the eye. Wittkower traces the evolution of this idea back to the Pythagoreans through Plato, who "in his Timaeus explained that cosmic order and harmony are contained in certain numbers." [2]
Alberti, whose architectural treatise De re aedificatoria (first printed in 1486) was certainly known to Palladio, is quite explicit on the subject, stating for example: "The very same numbers that cause sounds to have that concinnitas, pleasing to the ears, can also fill the eyes and mind with wondrous delight."[3] Palladio, on the other hand, seems rather ambivalent on the subject. While in his 1567 opinion on a model for a new cathedral for Brescia he said, "[J]ust as the proportions of voices are harmony to the ears, so those of measurement are harmony to the eyes…."[4] In his Quattro libri (1570), which is much less theoretical than Alberti's treatise, Palladio makes no explicit mention of analogies to music, not even when he states, "There are seven types of room that are the most beautiful and well proportioned and turn out better: they can be made circular, though these are rare; or square; or their length will equal the diagonal of the square of the breadth; or a square and a third; or a square and a half; or a square and two-thirds; or two squares." [5]
Even though Palladio enters the harmonic proportion debate only implicitly through his oeuvre, Wittkower makes the argument that Palladio's circle of scholars and artists, which included such architectural theorists as Giangiorgio Trissino and Daniele Barbaro, would have embraced the 'neo-Platonist' concept of harmonic proportions and would have influenced Palladio to use them in his architecture.
In the past two decades, architectural historians following in Wittkower's path (and thus often dubbed 'the Wittkowerians') have sought to better evaluate Palladio's use of harmonic proportions by analyzing the dimensions of his designs as given in Book II of the Quattro Libri. Through their study of the 44 plans of Book II, Deborah Howard and Malcolm Longair conclude, for example, that about 2/3 (65-70%) of the dimensions given are "harmonic numbers," whereas only 45% would be harmonic if Palladio picked dimensions at random. [6] They also find that, while harmonic numbers are fairly spread out among the plans of Book II, those plans which are completely harmonic were all designed after about 1556, and for patrons who may have shared an interest in musical theory.
Branko Mitrovic extends the analysis by considering heights of rooms as well as lengths and widths. He also gives a provocative explanation of how root-2:1 (one of the seven proportions Palladio touts as "most beautiful") can be viewed as a harmonic proportion since it corresponds to the augmented fourth of an equitempered scale, which was suggested by a contemporary of Palladio named Gioseffe Zarlino. Mitrovic concludes that "Wittkower's thesis…can be seen to be more consistent than it previously appeared." [7]
In my mind, however, Mitrovic makes a much more compelling pair of observations. First, he finds in Book II six unexplained (i.e., non-harmonic) proportions that approximate root-3:1, the closest being the large corner rooms of Palladio's most celebrated villa, the Villa Rotonda, which measure 26 by 15 (26/15 is within 0.07% of root-3 [8]). Mitrovic calls this proportion "triangulature" because root-3:1 is the ratio of the longer leg to the shorter leg in a 30°-60°-90° triangle (half of an equilateral triangle). It should be noted that Alberti describes precisely this construction of root-3 in his treatise, as well as the realization of both root-3 and root-2 as the diagonal of a cube and the diagonal of one of its faces, respectively (Fig. 3).
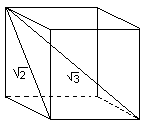
Figure 3
Perhaps Palladio was expressing a fondness for pure mathematics at least as much as an appreciation of harmonic proportions.The second, related, observation is equally compelling. Mitrovic first reminds us that Palladio describes and illustrates geometric constructions for the arithmetic mean (Fig. 4),
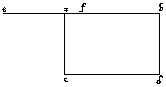
Figure 4
the geometric mean (Fig. 5)
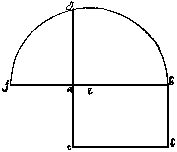
Figure 5
and the harmonic mean (Fig. 6),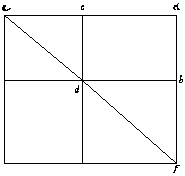 which Palladio proposes for use as
the heights of vaulted rooms (the length and width being the
two extremes of which the mean is taken):
which Palladio proposes for use as
the heights of vaulted rooms (the length and width being the
two extremes of which the mean is taken):
[W]e should make use of each of these heights depending on which one will turn out well to ensure that most of the rooms of different sizes have vaults of an equal height and those vaults will still be in proportion to them, so that they turn out to be beautiful to the eye and practical for the floor or pavement which will go above them….[9]
Again, the Villa Rotonda provides an example. Mitrovic observes that the height of each of the four corner rooms is given by the arithmetic mean, (26 + 15) / 2 = 20.5, so that each has a height to width ratio of approximately 1.3666. Moreover, the adjacent four rooms (the only other primary rooms on the piano nobile other than the central domed room; see Fig. 7), each of which measure 15 by 11, not only share a dimension with the corner rooms but are of proportion approximately 1.3636, which is within 0.2% of 1.3666. There is another crucial link between rooms that Mitrovic fails to observe, however: the diameter of the central domed room is 30, which is the hypotenuse of a (virtual) 30°-60°-90° triangle having 26 and 15 as its two legs (Fig. 8)!
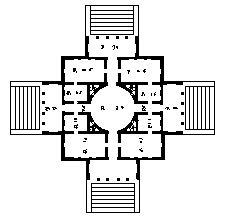 Figure 7 |
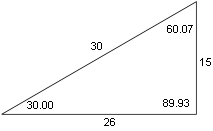 Figure 8 |
It seems highly unlikely that such closely interlocked mathematical puzzles would not be deliberate themes of Palladio's design.
Unfortunately, one can only conjecture on Palladio's intentions, given the lack of explicit references to music or mathematical theory in the Quattro Libri. It remains, then, to continue to gain evidence of Palladio's motivations and intentions from clues implicit in his work or based on what we know of his life experiences.
Such evidence is at the heart of a collaborative effort involving four workshop participants,stemming from the workshop. The project is to translate into English and annotate Silvio Belli's 1573 treatise on proportion, Della Proportione et Proportionalità. A mathematician, engineer, and cofounder of the Olympic Academy, Belli was a close friend of Palladio for many years. Exploring Belli's ideas on proportion may provide important insight into Palladio's own mathematical thinking. Surprised upon finding no English translation of Belli's treatise, I had approached Kim about this project just before the workshop. She accepted the invitation to be the principal translator after Vera, Rocco, and I gladly agreed to provide constructive criticism in order to assist her in honing the translation and commentary.
 In future visits
to the Villa Rotonda (and possibly other villas), I will take
the opportunity to measure the window and door openings in order
to analyze their proportions. This was motivated by observations
made during this workshop. David Speiser noted that the iron
grill in front of some of the windows at the Villa Rotonda seemed
to suggest a root-3 proportion having been employed (see Figure
7), though we were quickly able to deduce that the grill is not
composed of equilateral triangles as it first appeared. Even
so, this inspired me to photograph the window as carefully as
possible in order to avoid distortion, and up to the accuracy
of the photograph, the proportion of the window is 2:1. Vera
suggested that measuring the wall openings in Palladio's villas
might uncover new evidence for our analysis of Palladio's use
of proportion. One issue that will need to be addressed is how
to relate measurements taken in situ with idealized dimensions
from the Quattro libri.[10]
In future visits
to the Villa Rotonda (and possibly other villas), I will take
the opportunity to measure the window and door openings in order
to analyze their proportions. This was motivated by observations
made during this workshop. David Speiser noted that the iron
grill in front of some of the windows at the Villa Rotonda seemed
to suggest a root-3 proportion having been employed (see Figure
7), though we were quickly able to deduce that the grill is not
composed of equilateral triangles as it first appeared. Even
so, this inspired me to photograph the window as carefully as
possible in order to avoid distortion, and up to the accuracy
of the photograph, the proportion of the window is 2:1. Vera
suggested that measuring the wall openings in Palladio's villas
might uncover new evidence for our analysis of Palladio's use
of proportion. One issue that will need to be addressed is how
to relate measurements taken in situ with idealized dimensions
from the Quattro libri.[10]
Future workshops could provide the opportunity for gathering
additional evidence. Of course, the most direct benefit of a
future workshop will again be the exposure of the participants
to Palladio's exquisite designs, and to each other while experiencing
those designs. The opportunity to measure the window and door
openings of the Villa Rotonda is an added benefit (Fig. 9).
If these measurements prove to be useful for the analysis of Palladio's use of proportion, it would be most beneficial to conduct an exhaustive study of the wall openings of Palladio's villas.
ACKNOWLEDGMENTS
I would like to express my sincerest gratitude to Carroll William
Westfall for invaluable suggestions and references which continue
to bear fruit, and to Kim Williams for providing excellent advice,
friendly encouragement, and constant inspiration-and especially
for initially inviting me to explore the mathematics of Palladio's
villas. I gratefully acknowledge support in the form of grants
from the Graham Foundation for Advanced Studies in the Fine Arts
and Sweet Briar College.
NOTES
[1] The workshop in the summer of 1998 was partially
supported by grant #9846 from the Graham Foundation for Advanced
Studies in the Fine Arts. back to text
[2] Rudolf Wittkower, Architectural Principles in the Age of Humanism (New York: St. Martin's Press, 1988), p. 105. back to text
[3] Leone Battista Alberti, De re aedificatoria (On the Art of Building in Ten Books), trans. Joseph Rykwert, Neil Leach, and Robert Tavernor (Cambridge, Massachusetts: MIT Press, 1988), bk. IX, ch. v, p. 305. An understanding of Alberti's conception of concinnitas may be gleaned from the following quote from bk. IX, ch. v, p. 302: "It is the task and aim of concinnitas to compose parts that are quite separate from each other by their nature, according to some precise rule, so that they correspond to one another in appearance." See the glossary entry for this term, p. 421-422, for a more detailed discussion. back to text
[4] Bruce Boucher, Andrea Palladio: The Architect in
His Time (New York: Abbeville Press, 1994), p. 239. back
to text
[5] Andrea
Palladio, I quattro libri dell'architettura (The Four Books on
Architecture), trans. Robert Tavernor and Richard Schofield (Cambridge,
Massachusetts: MIT Press, 1997), bk. I, ch. xxi, p. 57. back
to text
[6] Deborah
Howard and Malcolm Longair, "Harmonic Proportion and Palladio's
Quattro Libri," Journal of the Society of Architectural
Historians, vol. 41, no. 2 (May 1982), pp. 121ff. The idea that
a single number can be harmonic -- or not harmonic -- is fallacious,
as they tacitly admit (p. 134), but they convincingly argue that
their system of harmonic numbers is a valid tool by which to
measure Wittkower's thesis vis-à-vis Palladio's plans.
back to text
[7] Branko
Mitrovic, "Palladio's Theory of Proportions and the Second
Book of the Quattro Libri dell'Architettura," Journal of
the Society of Architectural Historians, vol. 49, no. 3 (Sept.
1990), pp. 281-285. back to text
[8] This is
well within the allowed error tolerance of many rigorous statistical
experiments. back to text
[9] Andrea
Palladio, Quattro libri (trans. Robert Tavernor and Richard Schofield),
bk. I, ch. xxiii, p. 59. back to text
[10] Deborah
Howard and Malcolm Longair discuss the relative merits of measurements
obtained from the Quattro libri as opposed to those taken on
site; see "Harmonic Proportion," p. 117-118. back
to text
FOR FURTHER READING
Leone Battista Alberti, De re aedificatoria (On the
Art of Building in Ten Books), trans. Joseph Rykwert, Neil
Leach, and Robert Tavernor (Cambridge, Massachusetts: MIT Press,
1988). To order this book from Amazon.com, click
here.
Bruce Boucher, Andrea Palladio: The Architect in His Time (New York: Abbeville Press, 1994). To order from Amazon.com, click here.
Jay Kappraff, "Systems of Proportion in Design and Architecture and their Relationship to Dynamical Systems Theory", Symmetry: Culture and Science (The Quarterly of the Insternational Society for the Interdisciplinary Study of Symmetry-ISIS-Symmetry), vol. 10, no. 3-4: 299-316.
Andrea Palladio, I quattro libri dell'architettura (The Four Books on Architecture), Robert Tavernor and Richard Schofield, trans. (Cambridge, Massachusetts: MIT Press, 1997). To order from Amazon.com, click here.
Vera W. de Spinadel, "'Triangulature' in Andrea Palladio," Nexus Network Journal, vol. 1, (1999), pp. 117-119. To order, click here.
Stephen R. Wassell, "The Mathematics of Palladio's Villas," Nexus II: Architecture and Mathematics, Kim Williams, ed. (Fucecchio, Florence: Edizioni dell'Erba, 1998), p. 173-186. To order, click here.
Rudolf Wittkower, Architectural Principles in the Age of Humanism (New York: St. Martin's Press, 1988). To order this book from Amazon.com, click here.
RELATED
SITES ON THE WWW
Palladio's
Italian Villas
The
Palladio Museum
An
Itinerary of Villas and their Commissioners
Life of Palladio
Villa
Rotonda
Villa
Poiana
Villa
Pisani
Geométrica:
Arquitetos: Andrea Palladio
ABOUT THE AUTHOR
Steve Wassell received a B.S. in architecture in 1984, a Ph.D.
in mathematics (mathematical physics) in 1990, and an M.C.S.
in computer science in 1999, all from the University of Virginia.
He is a Professor of Mathematical Sciences at Sweet Briar College,
where he joined the faculty in 1990. Steve's primary research
focus is on the relationships between architecture and mathematics.
He has presented papers at Nexus 1998 and Nexus 2000, published
articles in The Mathematical Intelligencer and the Nexus Network
Journal as well as a book (with Kim Williams) entitled On Ratio
and Proportion (a translation and commentary of Silvio Belli,
Della proportione et proportionalità), and taught a course
at SBC entitled Architecture and Mathematics. Steve's overall
aim is to explore and extol the mathematics of beauty and the
beauty of mathematics. return to text
|
Stephen R. Wassell, "Mathematics of Palladio's Villas", Nexus Network Journal, vol. 1(1999), pp. 121-128. http://www.nexusjournal.com/Wassell.html |
Copyright ©1999 Kim Williams

