
|
Structural Stability and the Mathematics of
Motion in Medieval Architecture |
|---|
Rue des Caves
41800 Fontaine-les-Côteaux FRANCE
From a technological point of view, the nave of Saint-Etienne in Nevers is recognized as the earliest known example of a triple elevation beneath a high vault. Curiously, the church features minimal use of traditional buttressing, relying instead on stilted quadrant arches and blind wall arcades. A standard structural analysis reveals that the quadrant arches function as interior "flying buttresses." This is the earliest known Romanesque example and amply predates Gothic developments in the use of perpendicular counterthrust. Most surprisingly, from its apex to the ground, the vaults and support systems closely describe a parabolic arc.
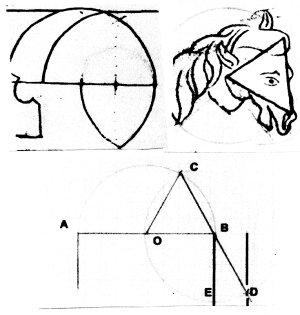
Technical drawing of arcs (Paris, B.n., ms. fr 19093, fol. 21) with horse's head (fol. 18v) and calculation of wall thickness. Drawing by Renaud Beffeyte
A long-term study of this eleventh-century French church suggests the builders had access to a higher level of mathematical knowledge than previously admitted for the period. Design analysis, based on a measured survey, reveals probable use of three linear measures to determine both the plan and elevation. In contrast to Gothic design methods using sequential rectangles, this Romanesque design can be laid out using just three measures to describe a series of intersecting arcs (or circles). While these measures have a certain arithmetic relationship, a geometric relationship such as the golden section is not immediately obvious.
The three measures were crucial for planning the interior length and width of the plan, the principal vault heights and, in particular, the thickness of walls. The builder's concern to define mural mass at the design stage implies an interest in the stability of three-dimensional solid structures. Since the resolution of dynamic forces at Nevers was unprecedented, we propose that the choice of distance intervals was a key factor. This paper proposes to study the geometrical relationships of the three measures, in terms of intersecting curves and straight lines, within the context of the history of mathematics. We propose to examine whether the determination of such measures was intended for predicting stable three-dimensional solid structures.
AUTHOR'S NOTE
The drawings accompanying this article
were drawn on paper by hand using only compass and straightedge.
The method qualifies as "constructive geometry," that
is moving from point to point, and seems to closely approximate
medieval building geometry. Subsequent analysis (by mathematical
calculation or by means of AutoCAD) has shown that the angles
of certain drawings are not regular. For example, the apex of
the triangle in fig. 3 is 105°, not 108°. But the medieval
mason did not use algebraic computation. And the ability to measure
or draw precisely with a total station and AutoCAD is not necessarily
appropriate to the medieval context -- which point should be
measured where walls lean and axes deviate? On the general subjectivity
of modern technology see Harrison Eiteljorg, II, "Measuring
with Precision and Accuracy", CSA Newsletter,
vol. XV, no. 1 (Spring 2002). Although it may not be "perfect,"
the proposed mnemonic device may nonetheless have existed as
such and served as the basis for determining three proportions
of "harmonic" relation; further research may tell us
more. To take a second example, the pentagram in fig. 9 has angles
of 34°, 37° and 35°, not 36°. Again while not
absolute in the modern computational sense, the geometry of fig.
9 based on the golden section rectangle nonetheless did exist
as such -- the sheep device was the "passport" of the
medieval mason -- according to the continuous oral tradition.
Although it may not land someone on the moon, this geometry sufficed
as a mnemonic device for construction. Moreover, the organic
quality of medieval building may be in part due to this built-in
kind of irregularity.
My discussion of tiers point (figs. 4, 8) may be ignored, however, since the deviation is well more than 1%. Finally, the argument needs to take into account the chronology of highly-developed siege machines such as the trebuchet. It is generally assumed that the trebuchet was introduced in Europe only after the 1099 crusade but there is some suggestion that after moving westwards from China, beginning in the sixth century, knowledge of the machine had reached Byzantium and Sicily by the ninth century. See recent summary with references to Villard, in Peter Vemming Hansen, "Experimental Reconstruction of a Medieval Trebuchet," Acta Archaeologica 63 (1992): 189-268.
ABOUT THE AUTHOR
Marie-Thérèse
Zenner is an American scholar
living and working in France. Recipient of numerous dissertation
grants including the Fulbright and Whiting, she received the
Ph.D. from Bryn Mawr College (Pennsylvania) in 1994 for a methodological
study on the comprehensive physical analysis of medieval stone
buildings. Associated with the CNRS in Poitiers (France) from
1994-2001, Dr. Zenner currently works as an independent historical
consultant for museums and cultural sites in Europe (with her
own agency, Villard Arts Inc). A new contributing editor for
medieval studies to Nexus Network Journal, she also directs the
annual conference program for AVISTA,
an international interdisciplinary society she co-founded in
1984. Dr. Zenner is editor-in-chief of a volume in memory of
Jean Gimpel (author of Les Bâtisseurs de Cathédrales),
AVISTA series, volume 2, in preparation for Ashgate Publishing
(England). Following a J. Paul Getty Postdoctoral Fellowship
in 1996-97 entitled "The Sciences of Measure in Romanesque
France between Vitruvius and Villard," Dr. Zenner has specialized
in the mathematics as well as the monumental archaeology of pre-Gothic
architecture, and more generally, the interrelationships of pre-modern
science, technology and architecture, in addition to the symbolic
traditions of astronomic-agronomic calendars in the pre-Christian
and Christian eras.
|
Marie-Thérèse Zenner, "Structural Stability and the Mathematics of Motion in Medieval Architecture", Nexus Network Journal, vol. 4, no. 3 (Summer 2002), http://www.nexusjournal.com/N2002-Zenner.html |

Search the NNJ