The vertical spiral of the distribution of leaves around the stems of certain plants ("the architecture of upright plants" [1]) exhibit what is sometimes called the "Ideal" (or "Fibonacci") Angle[2] as viewed from the top of the plant looking down.

The inverse angle of (Ö5+1) ÷ 2 of 360° is 137° 30' 27.95", and if the leaves of a plant were set round a straight stem at a divergence angle of about 137° 30' 28" (137. 5°), no two leaves would ever be exactly one over the other, which is generally the ideal condition. From this we deduce the fact that plants which utilize this angle to give the minimum superposition and maximum light exposure to their assimilating members are employing a leaf arrangement which may be expressed in terms of Fibonacci numbers.[3]

Simply stated, the golden section of the circumference of a circle is approximately 137. 5°
(137. 50776…° ) There are no exact constructions for this angle (most notably because, like p, it is irrational) that I'm aware of. However, I had the delight and good fortune to have found four drawings that come exceedingly close to it and that are generated from a master grid for the Ö2 rectangle. I have not done the calculations for the percent deviations, but the measures are virtually accurate. As a result, I am certain that the proofs would validate the careful constructions within an acceptable deviation that demonstrate that the relationships exist.[4]

Figure A

The Ideal Angle, phi or f of the circle, 360°/f (not to be confused with f of p, a totally different issue), angle AOZ, is shown in Figure A. We can find the golden section of almost anything having to do with time and space. The golden section of the circle seen here is quite unique and striking, and can sometimes even be recognized.[5]

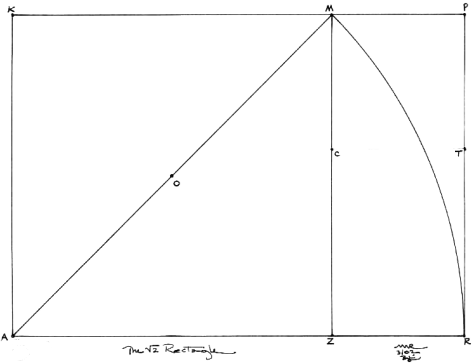
Figure B

Figure B is the Square Root Two (Ö2) Rectangle. This master grid contains:

• Square AKMZ, where AK = 1
• Diagonal of the square, AM; AM = AR= Ö2
• Ö2 rectangle, AKPR
• Theta (q) rectangle, ZMPR, which contains square, CMPT, and Ö2 rectangle, ZCTR (h = Ö2 +1).

Figures 1, 2, 3, and 4 will illustrate the four methods for creating the approximations of the Ideal Angle in the Ö2 rectangle. Before we begin, it is important to note that the demonstrations made here do not happen frequently. Although it is true that if one develops a sufficiently dense enough grid, possibilities can develop that could lead to many discoveries, what is being shown here is well outside the norm, especially because: a) only the basic elements of the grid are being used; and b) because the systems that develop are incommensurable. What is found here is unexpected in the extreme, as we find not one, but four, relationships with these two incommensurables, the Ideal Angle related to f, and Ö2.

METHOD I
This series of drawings actually began with an exploration of the centers of the circle/square progression within the rectangle (manifested by the square portion of the ever reducing theta rectangles within the field of the master rectangle). I was curious about what the straight line spiral looks like that develops from the centers of the squares, and to see what the advanced grid would look like as well.

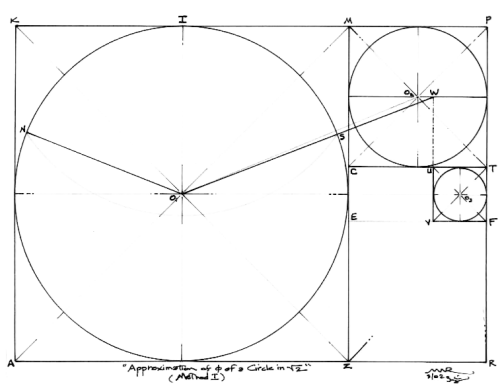
Figure 1

Figure 1 shows my original first three squares with centers, O¹, O² and O³. (The h rectangle can also be divided into squares on both ends and separated by a reciprocal h rectangle, which is the source of circle 3 and the procedure to continue the progression.) In my measurement of the angle tendered by the line, O¹O², to the vertical axis of the master circle, O¹. When I saw that it measured almost exactly 67.5°, I knew immediately that, doubled, the angle inside the circle would be an approximation of the Ideal Angle. The angle would be 135°, slightly less than the needed 137.507…°. To my enjoyment, I found that if I used an approximation for the golden section only to the tenths place, 1.6, it yielded this angle! Still, knowing that the angle needed to be about 2° greater for that "greater degree of perfection", so to speak, I looked at my grid again. I extended the left side of square, VUTF, to the horizontal diameter of circle, O², at point, W, and generated a line to W from O¹ to see what the new angle would be. O¹W subtends an angle of just about 68.75° to the vertical, by measurement. This angle doubled, NO¹S, is very near the Ideal Angle of 137.5°

METHOD II
Next, in the spirit of exploration, I followed a hunch concerning the extension of line NO to see if there may be something significant in another part of the grid construction that would yield line NO (half the Ideal Angle, along with its mirror symmetry line, OS) if Line NO were not present.

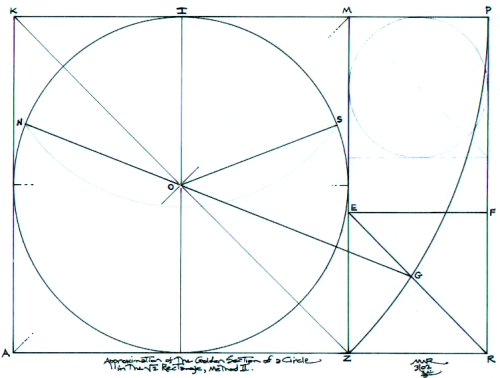
Figure 2

In Figure 2, I used the construction arc ZP and where it cuts the diagonal of the square, ZEFR, at point G. This point yields line NO by drawing through the center of the Master Circle, O¹. Again, from point I an arc can be swung from N through O to S to obtain this same very close approximation of the Ideal Angle.

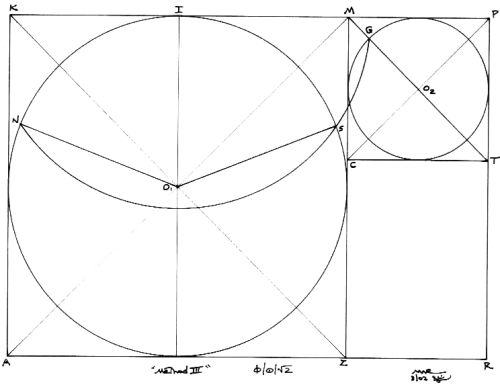
Figure 3

METHOD III
I next looked to the master circle O¹ within the master (generating) square, and what I call its "satellite", circle O², in the accompanying theta (q) rectangle ZMPR in Figure 3. By drawing the diagonals CP and MT of the square CMPT to generate the point G where the diagonal MT cuts the circle, I was able to swing the arc GN with its center at I. Again, the angle NS closely approximates the Ideal Angle, and is very nearly the same angle generated in the first two methods.[6] The same thing can be said for Method IV.

METHOD IV
Figure 4 was done as a curious venture to see if any further constructions existed to generate the angle. I did not think that there could possibly be any other points in the grid; I was already surprised to find three, let alone one! As can be seen in Figure 4, another possibility does indeed exist. Square VUTF in the reciprocal h rectangle, ECTF, (to theta rectangle, ZMPR) was drawn and the midpoint J of its side, VF was found. A line was then drawn to the mid point I of the side KM of the master square AKMZ. Line IJ cuts the circle O¹ at S and generates the Ideal Angle NO¹S once again.

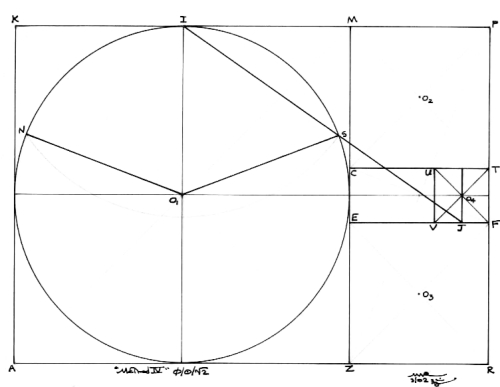
Figure 4

Perhaps if I were to continue, there would be other connections as well. I leave those possibilities to other adventuresome spirits while I go back to the drawing board to see what else geometry might be kind enough to teach me.

NOTES
[1] Michael Schneider in The Beginner's Guide to Constructing the Universe, p. 168. back to text

[2] Theodore Andrea Cook, The Curves of Life (New York: Dover Books, 1979), p.418. back to text

[3] Ibid., p.418. back to text

[4] I always invite associates, scholars, mathematicians, artists, designers, and architects to get in touch with me to do collaborative work on the constructions and principles I present in the column. back to text

[5] We can find a close approximation to this angle when we look at advertising showing the hands of traditional watches, which are almost always in this position. back to text

[6] As these drawings are done on tracing vellum, as overlays on the original drawing in Figure B, all four methods virtually lie any one over the other three. back to text

Copyright ©2005 Kim Williams Books