INTRODUCTION
Plato, acting as a kind of Socratic midwife presenting problems and puzzles in much the same way to his readers as he did in the Academy, carefully secreted a most profound Pythagorean doctrine into his written dialogues. He did so for those capable of "abducting" [1] the solution in light of the hints he provides. Here I will attempt to uncover the nature of Plato's Second Principle, known as the Indefinite Dyad, sometimes called the Greater and the Lesser, and its relation to the Golden Section, f. The crux of my hypothesis is the following:

This is, to my knowledge, a novel hypothesis, and my goal in this paper is to argue its potential for validity. Recall the following facts:

.

Given these facts and the hypothesis above, we have:

The fact that the ratio of the Greater to the Lesser is f² and not f is crucial to my interpretation of the Indefinite Dyad. The importance of these relationships will become clear only after a review of some pertinent classical Greek philosophy.

THE PHILOSOPHICAL BACKGROUND
Before starting, I offer the following overview, the details of which will be discussed in the rest of the article. An application of abductive reasoning to Plato's puzzles in the dialogues leads to the solution that the Divided Line in the Republic is constructed using a series of Golden Cuts (i.e., divisions in extreme and mean ratio). This leads to the discovery that there is a more primitive form than the Ö2 and Ö3 ratios (the roots inherent in the elementary triangles of the Timaeus), and that this form is based in the Golden Section. In fact, as we shall see, the discovery is that the Golden Section can actually be employed in the construction of these roots. And put simply, abductive reasoning is the method by which one arrives at the solution that the Golden Section and its reciprocal are in fact the Greater and the Lesser of the Indefinite Dyad.

Plato, primarily as a proponent of Pythagorean philosophical doctrines,[2] was very careful with what he did and did not reveal, being under an apparently severe oath of secrecy. Both his writings and lectures are enigmatic, and he only very carefully and subtly provides the clues with which the observer may be capable of uncovering the inner doctrines for themselves. His method in the written dialogues appears to be similar to his reported approach in the Academy, where he would propose the problem to be solved. He would present the problem, puzzle, anomaly, apparent contradiction or incomplete result, intending that the attentive student would abduct an explanatory hypothesis. Thus, the underlying intention was to get the observer (Academy member or dialogue reader) to abduct (hypothesize) an appropriate solution or answer, rather than to accept the dead end, apparent contradiction or incomplete result.

There are several Platonic puzzles and unsolved issues. Some of these arise within the dialogues and others in remarks made by Aristotle and early commentators regarding Plato's doctrines. When several of the key puzzles are viewed in conjunction, they help point in the direction of the required solution. In particular, I will argue that the Timaeus and the Republic together point to the Golden Section. The Timaeus does so by the conspicuous absence of the Golden Section, since Plato provides no appropriate elementary triangle for the construction of the Dodecahedron, often considered the most sublime of the five solids. And in the Republic, Plato subtly and with great economy embeds the Golden Mean in the beautiful ontology of his Divided Line analogy. Together the Timaeus, Republic, and Parmenides 133b ("worst difficulty argument") point to continuous geometric proportion as that which binds together Plato's realms of Being and Becoming. And finally, as we shall see, continuous geometric proportion and the Golden Mean are embedded in Plato's most important ontological principles, the One and the Indefinite Dyad. This should have special ramifications for a whole family of issues surrounding the role of geometry in aesthetics.[3]

Aristotle makes it eminently clear that within the Academy, Plato professed Two Principles, principles that were involved in the construction of the Forms (Universals or Archetypal Numbers), as well as the Sensibles (Particulars) of our Empirical World. The First Principle is generally acknowledged. It is the Good of Plato's Republic, also referred to in the Academy in its more mathematical context as the One. The other Principle was usually referred to as the Indefinite Dyad, and at times as the Greater and the Lesser, Excess and Deficiency, or the More and the Less. Occasionally one would see the Two Principles contrasted in terms of the One as Equality and the Indefinite Dyad as embodying Inequality.

Although there are important references to this Second Principle in the dialogues (especially the Philebus), there is no real clarity as to its meaning and definition. It is an understatement to suggest that Plato was reserved in his references towards it. In fact, when he apparently lectured on the subject of the One and the Indefinite Dyad in his so-called Agrapha Dogmata (Unwritten Lectures) or Lectures On the Good, he continued to veil his presentation in secrecy. Simplicius records, in his Commentarius in Physica 453.25-30:

They say that Plato maintained that the One and the Dyad were the First Principles, of Sensible Things as well. He placed the Indefinite Dyad also among the objects of thought and said it was Unlimited, and he made the Great and the Small First Principles and said they were Unlimited, in his Lectures On the Good; Aristotle, Heraclides, Hestiaeus, and other associates of Plato attended these and wrote them down in the enigmatic style in which they were delivered [Barnes 1984: 2399 (emphasis added)].

And as these Two Principles were ontologically prior to and causally involved in the manifestation of both the Forms and Sensible things, it should not be surprising that Plato held them to be of the utmost importance. Thus we learn from Aristotle's pupil and commentator, Alexander, that these Two Principles were "more important than the Ideas" (Commentarius in Metaphysica 88.1) [Barnes 1984: 2440].

Now according to Aristotle and others, what Plato presented to members of the Academy and in public lectures was not always identical to the content of the written dialogues. We learn from Simplicius that:

Alexander says that "according to Plato the One and the Indefinite Dyad, which he spoke of as Great and Small, are the Principles of all things and even of the Forms themselves." So Aristotle reports also in his books On the Good. One might also have got this from Speusippus and Xenocrates and the others who attended Plato's course On the Good [Simplicius on Aristotle's Physics 187a12, quoted in Kramer 1990: 203].

Thus, there is considerable evidence of Plato avowedly professing that there are the Two Principles of the One and the Indefinite Dyad.

The great mystery has always been, what exactly does Plato mean by the Indefinite Dyad, or as he called it, Excess and Deficiency, or the Greater and the Lesser. Aristotle does tell us:

Since the Forms are the causes of all other things, he thought their elements were the elements of all things. As matter, the Great and Small were Principles; as substance, the One; for from the Great and the Small, by participation in the One come the Forms, the Numbers [Metaphysics 987b19-22].

And of course all Sensible objects of this world are derivative from these original Principles via the Forms or Numbers.

Now in the Timaeus, Plato boldly hints at the deeper revelations to be gained by those who carefully pursue his clues and incomplete analyses. He poses the question:

What are the most perfect bodies that can be constructed, four in number, unlike one another, but such that some can be generated out of one another by resolution? … If we can hit upon the answer to this, we have the truth concerning the generation of earth and fire and of the bodies that stand as proportionals between them [Timaeus 53e; emphasis added].

As Keith Critchlow indicates:

This demonstration of the continuing pre-eminence of proportion is followed by a curious "evasion," which we can only assume is a covering up of the fifth body [Critchlow 1994: 156; emphasis added].

Plato gives us the Ö2 triangle for the construction of the Cube, and the Ö3 triangle for the construction of the Tetrahedron, Octahedron and Icosahedron. But the triangle (or the root numbers embedded in it) necessary for the construction of the Dodecahedron is most conspicuously absent. Regarding the Ö2 and Ö3 primitive triangles, however, Plato states cryptically (and yet very revealingly for the astute student):

These then... we assume to be the original elements of fire and other bodies, but the principles which are prior to these Deity only knows, and he of men who is a friend of Deity.… [A]nyone who can point out a more beautiful form than ours for the construction of these bodies shall carry off the palm, not as an enemy, but as a friend.... [H]e who disproves what we are saying, and shows that we are mistaken, may claim a friendly victory [Timaeus 53a-54b; emphasis added].

The missing triangle for the construction of the Dodecahedron must involve (purely from mathematical considerations) the Golden Section. But why is the Golden Section to be so protected within the Pythagorean tradition? I would like to propose here that for Plato it is its ontological priority over the Forms, the Numbers. It is the discovery that it is embedded in, if not the very basis of, the Principle of the Indefinite Dyad that is so remarkable. And as we shall see, it is this Principle along with the One that is involved in a deeper revelation regarding continuous geometric proportion.

In the Timaeus, Plato states:

Two things cannot be rightly put together without a third; there must be some bond of union between them. …and the fairest bond is that which makes the most complete fusion of itself and the things which it combines, and proportion (analogia) is best adapted to effect such a union. For whenever in any three numbers, whether cube or square, there is a mean, which is to the last term what the first term is to it, and again, when the mean is to the first term as the last term is to the mean - then the mean becoming first and last, and the first and last both becoming means, they will all of them of necessity come to be the same, and having become the same with one another will be all one [Timaeus 31b-32a].

Now following the Pythagoreans, Plato places a great deal of emphasis on numbers, ratio (logos), and proportion (analogia). As Aristotle attests in several places, "…those who speak of Ideas say the Ideas are Numbers" (Metaphysics 1073a18-20). And again:

[T]he numbers are by him [Plato] expressly identified with the Forms themselves or principles, and are formed out of the Elements (i.e., Principles of the One and Indefinite Dyad). [De Anima 404b24].

In the Republic, Plato presents a series of similes or analogies with the apparent purposes of:

1. indicating a kind of ontological proportion linking together his worlds of Being and Becoming, and
2. providing an epistemological framework for attaining deeper insights into the nature of reality.

He does this with the Sun Analogy (Republic 502d-509c), the Divided Line (509d-511e), and the Cave (514a-521b). I have discussed these metaphors elsewhere at length [Olsen 1983; 2002], and will be concerned here primarily with how the Divided Line assists in penetrating into the possible nature of the Indefinite Dyad.

THE DIVIDED LINE AND THE "SAYRE CHALLENGE"
Plato begins by saying:

Suppose you have a line divided into two unequal parts, to represent the Visible and Intelligible orders, and then divide the two parts again in the same ratio (logos)… in terms of comparative clarity and obscurity [Republic 509D].

Usually when commentators attempt to determine how the line is to be divided, they fail to first fully consider the underlying significance of Plato asking the reader to divide the line unevenly. Now it seems clear to me that if Plato is concerned primarily about continuous geometric proportion, as he appears to assert in Timaeus 31b-32a, then there is one and only one way to divide a line (and it is unevenly) such that you immediately have a continuous geometric proportion, and that is with a division in extreme and mean ratio, or what we now call a Golden Cut: [4]

Plato then asks us to cut each of those two segments again in the same ratios, namely Golden Cuts. In effect what Plato is asking us to do is to perpetuate the continuous geometric proportion into the four subdivisions of his Divided Line. What he has effectively done through a series of Golden Cuts is to bind his so-called Intelligible and Sensible Worlds (and their subdivisions) together through continuous geometric proportion employing the Golden Section.

Kenneth M. Sayre of the University of Notre Dame, in his 1983 book, posed a very interesting challenge to anyone who would propose a Golden Section solution to Plato's Divided Line. I will call it the "Sayre Challenge." He writes:

It is (barely) possible that Plato had the golden section (or golden rectangle) in mind when he constructed the Divided Line, and thought of its unique aesthetic qualities as somehow reflecting the Good as the ideal of beauty. The commentator convinced of this would have the formidable job on his hands of making sense of the extended equality,

A:B = C:D = (A+B) : (C+D) = (C+D) : (A+B+C+D),

which results from this interpretation [Sayre 1983: 304; emphasis added].

I accept the challenge. In fact it will assist us in explicating the underlying significance of the Indefinite Dyad and the One. Let us take a Pentagram, which inherently contains numerous Golden Cuts, and extract one of its lines while retaining its points of intersection.

Thus, we have line ab, which has Golden Cuts at points c and d.

Next take a pair of compasses and, rotating line segment cd (at point c), cut line ab at point e.

One consequence of this construction is what some have referred to as the "anomaly" that line segments dc and ce must be equivalent. Sayre states:

While many commentators have noticed this anomaly, most are of the opinion that Plato either did not notice it himself or did not acknowledge it…. Whether the anomaly had any significance for Plato beyond that of an untoward mathematical consequence seems conjectural at best [Sayre 1983: 303].

I want to suggest that, to the contrary, the abductive solution to this so-called anomaly helps lead to the most fruitful insights. Plato knew exactly what he was doing. He was very subtly embedding the Indefinite Dyad into his Divided Line, expressing it through continuous geometric proportion.

I propose that the inner two line segments dc and ce should be seen as each representing Unity or One. Let us label the line in a manner consistent with the "Sayre Challenge", with A being the smallest and D the largest. Given that segments B and C are equal (each being 1), it turns out that D will be f, the Greater, and A will be 1/f, the Lesser.

Thus, D : C :: B : A is none other than f : 1 :: 1 : 1/f, i.e., Greater : One :: One : Lesser.

In the Statesman, Plato suggests that:

It is in this way, when they preserve the standard of the mean that all their works are good and beautiful…. The greater and the less are to be measured in relation, not only to one another, but also to the establishment of the standard of the mean…. [T]his other comprises that which measures them in relation to the moderate, the fitting, the opportune, the needful, and all the other standards that are situated in the mean between the extremes [Statesman 284a1-e8; emphasis added].

This agrees with my hypothesized associations. The Greater and the Lesser are to be related not only to one another, Greater : Lesser (a single proportion exhibiting the f² ratio), but also to the standards that are situated in the mean between the extremes, Greater : One :: One : Lesser (a continued proportion exhibiting the f ratio).[5]

We can now verify the "Sayre Challenge":

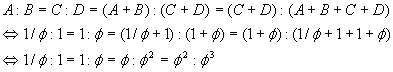
(here we have used the facts that 1/f + 1 = f, 1 + f = f², and f + f² = f³).

The Divided Line presents Plato's Two Principles, both the One and the Indefinite Dyad. And its accomplishment is that it effectively counters the "worst difficulty" argument of Parmenides 133b, i.e., the argument that there is no connection between the Intelligible Realm (segments D and C) with the Visible Realm (segments B and A). The solution is that the two Realms are bound together through continuous geometric proportion. And not only that, but the powers of the Golden Ratio are carried into the Visible Realm as a kind of enfolded Implicate Patterned Order.[6]

DERIVATION OF THE ROOTS OF 2 AND 3
There is a second part to this story. While investigating my intuition that the Golden Section is at the center of Plato's work, especially after finding it in the Divided Line (and perceiving the relevance of its absence in the Timaeus), I kept an eye out for any further subtle clues. It is interesting that Alexander in his Commentary of the Metaphysics, retains from Aristotle this very telling aspect about Plato's theory:

Thinking to prove that the Equal and Unequal [other names for One and Indefinite Dyad] are first Principles of all things, both of things that exist in their own right and of opposites...he assigned equality to the monad, and inequality to excess and defect; for inequality involves two things, a great and a small, which are excessive and defective. This is why he called it an Indefinite Dyad - because neither the excessive nor the exceeded is, as such, definite. But when limited by the One the Indefinite Dyad, he says, becomes the Numerical Dyad [Barnes 1984: vol. 2, 2398; emphasis added].

In other words, the whole number 2 can be generated from the Indefinite dyad. Indeed, recalling that Greater - Lesser = 1, we have Greater + Unity - Lesser = 2.

Now the real secret of Plato's Indefinite Dyad (in addition to generating the whole numbers) is that it may be employed to derive the other crucial roots (Ö2 and Ö3) necessary for the construction of four of the five Platonic solids.

The following construction is the result of carefully combining two insights, one that I had regarding Ö3, and one that Mark Reynolds shared with me regarding Ö2. While contemplating the nature of the Indefinite Dyad, which I had already decided must be the Golden Section and its reciprocal, I had a dream in which I saw the Greater and the Lesser as the legs of a right-angled triangle of which the hypotenuse was Ö3. I jumped out of bed and grabbed a pair of compasses, straightedge and pencil. I did the construction and lo and behold it was true (as we'll verify mathematically below).

Then a year later I had the good fortune of meeting Mark Reynolds. I shared this construction with him, and he in turn showed me how Ö2 was derivable, in a very similar manner, from the Lesser and the square root of the Greater as legs of a right-angled triangle.[7] (In both cases I was attending the KAIROS Summer School studying under Dr. Keith Critchlow and John Michell - Buckfast Abbey in Devon, England in 1997, and Crestone, Colorado in 1998.)

The construction of the Indefinite Dyad Template follows. Though the construction has already proven to harbor many wonderful properties, notice in particular the Quadrilateral DKMH, which acts as a kind of ontological entheogenomatrix.[8] Because of its morphology and seemingly sublime function, I propose to name it the "Golden Chalice of Orion".

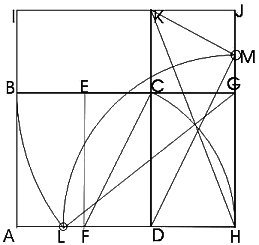
1. Construct Square ABCD with side AB = 1.
2. Construct the Golden Rectangle ABGH from Square ABCD using diagonal FC.
3. Construct Square AIJH by extending line AB to I, and line HG to J (in both cases extend the line lengths by the equivalent of DH or 1/f), and connect I to J.
4. AH = AI = IJ = HJ = f.
5. Extend line DC intersecting line IJ at K.
6. DK = f.
7. DH = KJ = CK = 1/f.
8. Cut line AH at L by rotating side GB (at point G). Using the Pythagorean Theorem on right triangle GHL, since GL = f, GH = 1, and 1 + f = f², we obtain HL = Öf.
9. Cut line HJ at M by rotating line HL (at point H); HM = Öf.
10. Using the Pythagorean Theorem, DH² + HM² = DM²; thus we have,
    

    (1/f)2 + (Öf)2	= DM2
    1/f2 + f	= DM2
    (1 - 1/f) + (1/f + 1)	= DM2
    2	= DM2

    so that DM = Ö2 (here we have used the facts that 1/f² + 1/f=1, and 1/f +1=f).[9]
11. Using the Pythagorean Theorem, DH² + DK² = KH²; thus we have,
    

    (1/f)2 + (f)2	= KH2
    1/f2 + f2	= KH2
    (1 - 1/f) + (1 + f)	= KH2
    (1 - 1/f) + (1 + 1/f + 1)	= KH2
    3	= KH2

    
    
    so that KH = Ö3 (here we have used the facts that 1/f² + 1/f=1, and 1/f +1=f, and 1 + f = f²).

(For completeness, we note that KM » 0.708, which is within 0.2% of Ö2/2.) The amazing fact is that the two diagonals of the "Golden Chalice of Orion" are precisely Ö2 and Ö3!

Hence, Ö2 and Ö3 are ultimately derivable from the Greater (DK = f) and the Lesser (DH = 1/f).[10] As a result, the Indefinite Dyad gives rise to the roots that are employed in the construction of the Cube, Tetrahedron, Octahedron and Icosahedron. And of course this Second Principle is directly related to the derivation of the Dodecahedron. As such, the One and Indefinite Dyad were for the Pythagorean Plato the Principles behind all of existence. In the end, I suspect that this was the great Pythagorean secret that Plato could not openly reveal, but only hint at, expecting his attentive followers to abduct the solution. We begin to see why Plato was so careful not to reveal the real nature of the Golden Section and its reciprocal, respectively the Greater and the Lesser.

NOTES
[1] This method of inference has been variously described by one of its great exponents, the philosopher/ mathematician Charles Sanders Peirce, as abduction, retroduction, or novel reasoning. Peirce maintained that he rediscovered the abductive reasoning process in the works of Plato and Aristotle. In the Academy, problems that required abductive solutions included, for example, geometric problems regarding the Golden Section, the Delian Problem of doubling the cube, "reduction" of one problem to another, and the attempt to "save the appearances" of the apparent irregular motion of the planets. The last resulted in a magnificent abduction by Eudoxus of his explanatory hypothesis of concentric spheres. As for the abductive reasoning process itself, see [Olsen 1983: 8-44; Olsen 2002: 85-99]. return to text

[2] I have argued this point exhaustively elsewhere, and would at this stage simply refer the reader to my dissertation [Olsen 1983], especially pp. 45-121. return to text

[3] It should be noted that there is definite evidence that Plato and his pupils were working with the Golden Section in the Academy. Heath relates, "We are told by Proclus that Eudoxus 'greatly added to the number of the theorems which Plato originated regarding the section, and employed in them the method of analysis [abduction].' It is obvious that the section was some particular section which by the time of Plato had assumed great importance; and the one section of which this can safely be said is that which was called the 'golden section,' namely the division of a straight line in extreme and mean ratio which appears in Eucl. II. 11 and is therefore most probably Pythagorean"[1956: v. 1, 137]. return to text

[4] Others have proposed the principle of the golden section in the Divided Line (see [Brumbaugh 1954] and [Des Jardins 1976]) or a Fibonacci approximation to it [Dreher 1990]. But these prior attempts do not embody the essential features of the Greater and Lesser (Indefinite Dyad) in relation to the One, as I depict them below. For a critique of the sufficiency of earlier arguments (taken individually) that attempt to establish the golden sectioning of the Divided Line, see [Balashov 1994]. return to text

[5] We could also simply begin with the line as Unity, and then do the subsequent cuts. The initial golden cut of the line would then give us a longer and a shorter segment, namely, 1/ f and 1/f², and hence, (1/f) : (1/f²) would be in f ratio. I suspect that the understandable mistake of earlier commentators who were close to uncovering Plato's mystery, and hence the failure to notice the actual relationship between the Greater and the Lesser, follows from the tendency to associate Plato's Greater of the Indefinite Dyad with the "greater" of the two line segments, and the Lesser of the Indefinite Dyad with the "lesser" of the two line segments. With my interpretation, when we divide the line in this way, Unity becomes the "Greater," 1/ f becomes the "Mean," and 1/f² becomes the "Lesser," relatively speaking. If again, we proceed further with this initial golden cut of a line of Unity, and do our subsequent two golden cuts, we discover that the four resulting line segments are in the following continued proportion: (1/f²) : (1/f³) :: 1/f³ : 1/f⁴. Here, relatively speaking, 1/f² "acts" as the Greater, 1/f³ "acts" as the Mean, and 1/f⁴ "acts" as the Lesser. The relation here of the Greater to the Mean, and the Mean to the Lesser, is again the f ratio. And 1/f² (the Greater) in relation to 1/f⁴ (the Lesser in this context) is f². The advantage of portraying the divisions of the line as I do in this paper, is simply to more clearly reveal the underlying essence of the ratios, as they reflect the One and the Indefinite Dyad, i.e., Greater : 1 :: 1 : Lesser. Otherwise there is a tendency to overlook the crucial f² relationship between the Greater and Lesser that lies at the heart of this paper. return to text

[6] Here I am thinking of the Implicate Order that David Bohm, the physicist, suggested is enfolded into the outer Explicate Order of our world. This "patterned order" enfolded into Nature appears to be closely related to the continuous geometric proportion of the One and Indefinite Dyad as expressed, for example, in Fibonacci and Lucas whole number approximations in minerals, plants, animals, microtubules and DNA. See, for example, [Bohm 1980; Dixon 1992; Goodwin 1994; Penrose 1994; Martineau 1995]. return to text

[7] Neither Mark nor I labor under any false illusion that we have discovered these things; we have simply rediscovered them independently. Perhaps we are uncovering what for many in the past may have been restricted or esoteric knowledge. return to text

[8] Plato's ontology is based upon his Pythagorean belief that the Divine manifests throughout our world through the Numbers. Thus, he appears to be suggesting that the Principles of the Numbers, namely the Indefinite Dyad in relation to the One, generate or unfold the Divine within all things through this number matrix. During this construction, I would ask the reader to keep in mind a very important comment by Johannes Kepler: "Geometry has two great treasures: one is the theorem of Pythagoras; the other the division of a line into extreme and mean ratio [golden cut]. The first we may compare to a measure of gold; the second we may name a precious jewel" [quoted in Hambidge 1920]. This construction in effect embodies the application of these "two great treasures". return to text

[9] This is Mark Reynolds's very important contribution that allows this "Platonic Template" to work. return to text

[10] Notice also the relationship between the sides of the three squares, AI : AB : CK. They are in the continuous geometric proportion, f : 1 : 1/f. Thus they perpetuate the f relationship. In the case of the areas of the three squares, we have the f² relationship perpetuated throughout. Square AIHJ : Square ABCD : Square CKJG = f² : 1 : 1/f². return to text

REFERENCES
Balashov, Yuri. 1994. Should Plato's Line be Divided in the Mean and Extreme Ratio? Ancient Philosophy 14: 283-295.

Barnes, Jonathan, ed. 1984. The Complete Works of Aristotle, vol. 2. Princeton: Princeton University Press.

Bohm, David. 1980. Wholeness and the Implicate Order. London: Routledge & Kegan Paul.

Brumbaugh, Robert. 1954. Plato's Mathematical Imagination. Bloomington: Indiana University Press.

Cairns, Huntington and Edith Hamilton, eds. 1971. The Collected Dialogues of Plato. Princeton: Princeton University Press.

Condat, Jean-Bernard, ed. 1988. The Golden Section and Music. Frankfurt: Verlag Peter Lang.

Critchlow, Keith. 1963. Order in Space. New York: Thames and Hudson.

Critchlow, Keith. 1994. The Platonic Tradition on the Nature of Proportion. Pp. 133-168 in Homage to Pythagoras, C. Bamford, ed. New York: Lindisfarne Press.

Des Jardins, G. 1976. How to Divide the Divided Line. Review of Metaphysics 29: 483-496.

Dixon, Robert. 1992. Green Spirals. Pp. 353-368 in Spiral Symmetry, I. Hargittai & C.A. Pickover, eds. River Edge, NJ: World Scientific.

Dreher, John Paul. 1990. The Driving Ratio in Plato's Divided Line. Ancient Philosophy 10: 159-172.

Dunlap, Richard A. 1997. The Golden Ratio and Fibonacci Numbers. River Edge, NJ: World Scientific.

Fideler, David. 1993. Jesus Christ, Sun of God. Wheaton, Illinois: Quest Books.

Goodwin, Brian. 1994. How the Leopard Changed Its Spots. New York: Simon & Schuster.

Hackforth, R., trans. 1972. Plato's Phaedo. Cambridge: Cambridge University Press.

Hambidge, Jay. 1920. The Elements of Dynamic Symmetry: the Greek Vase. New Haven: Yale University Press.

Heath, Thomas L. 1956. The Thirteen Books of Euclid's Elements. 3 vols. 2nd ed. 1926. Rpt. New York: Dover Publications.

Herz-Fischler, Roger. 1987. A Mathematical History of the Golden Number. New York: Dover Publications.

Kirk, G.S. and R.E. Raven. 1975. The Presocratic Philosophers. Cambridge: Cambridge University Press.

Koshy, Thomas. 2001. Fibonacci and Lucas Numbers with Applications. New York: John Wiley & Sons.

Kramer, H.J. 1990. Plato and the Foundations of Metaphysics. J.R. Caton, ed. and trans. New York: State University of New York Press.

Kuhn, Thomas. 1970. The Structure of Scientific Revolutions. Chicago: Chicago University Press.

Martineau, John. 1995. A Book of Coincidence. Powys, Wales: Wooden Books.

Michell, John. 1988. The Dimensions of Paradise. London: Thames and Hudson.

Glenn R. Morrow. trans. 1992. Proclus: A Commentary on the First Book of Euclid's Elements. Princeton: Princeton University Press.

Mueller, Ian. 1992. Mathematical method and philosophical truth. Pp. 170-199 in The Cambridge Companion to Plato. Richard Kraut, ed. Cambridge: Cambridge University Press.

Olsen, Scott A. 1983. The Pythagorean Plato and the Golden Section: a Study in Abductive Inference. Ph.D. Dissertation, University of Florida.

Olsen, Scott A. 2002. Plato, Proclus and Peirce: Abduction and the Foundations of the Logic of Discovery. Pp. 85-99 in Neoplatonism and Contemporary Thought, Part One. R. Baine Harris, ed. New York: State University of New York Press.

Pacioli, Luca. 1982. De Divina Proportione. Milano: Silvana Editoriale.

Peirce, Charles S. 1931-1958. Collected Papers of Charles Sanders Peirce, 8 vols. A.W. Burks, C. Hartshorne, and P. Weiss, eds. Cambridge: Harvard University Press.

Penrose, Roger. 1994. Shadows of the Mind. Oxford: Oxford University Press.

Sayre, Kenneth M. 1983. Plato's Late Ontology: A Riddle Resolved. Princeton: Princeton University Press.

Schwaller de Lubicz, R.A. 1998. The Temple of Man. Deborah Lawlor and Robert Lawlor, trans. Rochester, Vermont: Inner Traditions.

Stewart, Ian. 1998. Life's Other Secret. New York: John Wiley & Sons.

Taylor, A.E. 1926. Forms and Numbers: A Study in Platonic Metaphysics (I). Mind 36: 12-33.

Taylor, A.E. 1928. A Commentary on Plato's Timaeus. Oxford: Oxford University Press.

Taylor, Thomas. 1804. The Works of Plato, 5 vols. London: R. Wilks.

Taylor, Thomas. 1983. The Theoretic Arithmetic of the Pythagoreans. York Beach, Maine: Samuel Weiser.

Thomas, Ivor. ed. 1957. Greek Mathematical Works, vol. 2. Cambridge: Harvard University Press.

Thompson, D'Arcy Wentworth. 1928. Excess and Defect: Or the Little More and the Little Less.
Mind 38: 43-55.

Thompson, D'Arcy Wentworth. 1992. On Growth and Form. New York: Dover Publications.

ABOUT THE AUTHOR
Scott A. Olsen is Associate Professor of Philosophy & Comparative Religion at Central Florida Community College, and a member of the Florida Bar. He received his B.A. in Philosophy from the University of Minnesota in 1975 where he wrote his honors thesis on "Platonic Aesthetics" under the tutelage of geometry professor, artist and author Dan Pedoe. He received his M.A. in Philosophy in 1977 from Birkbeck College, University of London where he studied Plato & Aristotle with David Hamlyn, and philosophy of space-time with the physicist David Bohm. At the University of Florida he received his J.D. in 1982 and his Ph.D. in Philosophy in 1983. In 1990 he was elected President of the Florida Philosophical Association. In 1992 he received an NEH Grant to spend 8 weeks studying the "Esoteric Dimension of Religion" with Huston Smith at Berkeley. Scott has presented numerous papers and lectures internationally centering on Plato, Neoplatonism, the Golden Section, transpersonal states of consciousness, the esoteric dimension of the world's wisdom traditions, and recently began presenting workshops in Sacred Geometry.

Copyright ©2005 Kim Williams Books