Transformational Geometry
and the Central European Baroque Church
John Clagett, Architect
Oakland, California, USA
 The Central
European Baroque church (CEBc) appears to be in endless conflict
with itself: at once unified and chaotic, continuous and fragmented.
Architects strived for Gesamtkunstwerk, architecture
and the plastic arts merging into a symphonic whole, and Zweischaligkeit,
in which contrasting tectonic systems coexist as a composite,
dissolving sharply-defined boundaries. The elements eternally
approach singularity: a dynamic continuum.
The Central
European Baroque church (CEBc) appears to be in endless conflict
with itself: at once unified and chaotic, continuous and fragmented.
Architects strived for Gesamtkunstwerk, architecture
and the plastic arts merging into a symphonic whole, and Zweischaligkeit,
in which contrasting tectonic systems coexist as a composite,
dissolving sharply-defined boundaries. The elements eternally
approach singularity: a dynamic continuum.
A look at scientific/mathematical developments
of the 1600's and 1700's helps place the CEBc in context: Desargues,
Newton, Leibniz and Descartes all dealt with theories of synthesis
and convergence. The effect of the new mathematical ideas was
on architecture was a gradual transformation of space from pure,
static and isolated to composite, dynamic and interpenetrating.
Architects used geometrical methods as plan generators. Transformational
operations were of utmost importance, including area, rotation,
reflection, translation, and coordinate transformation.
Rotation is present throughout the underlying planning geometry
of St. Michaelskirche, Berg am Laim (1744). The ceiling plan of
Neumann's WÀGÀrzburg Residenz Hofkirche (1733) demonstrates
both rotation and reflection. Another operation, Borrominian
transformation, describes the mutation of a rectilinear
spatial organization into an equivalent curvilinear structure,
while maintaining the starting rectilinear diagram, as in Dientzenhofer's
St. Niklas in Prague (1711.) Dilatation is also
present in the CEBc, as in Neumann's Church of the Holy Cross
at Neresheim, where the choir/altar half of the church is narrower
than its nearmirror image. A parallel may be drawn between the
mathematics and the architecture of the age. Descartes' fusion
of number and geometric form in his Géom&eacut;trie
may be likened to the ability to fuse and merge elements of
the architecture such as center and transept: both reinforce a
continuity previously unknown. In Architettura civile,
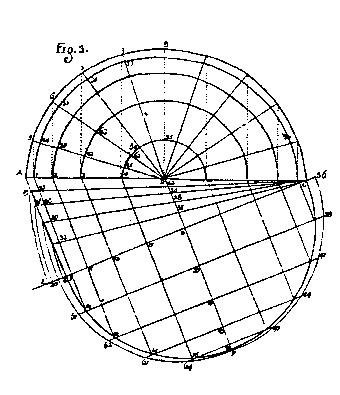
Guarini included a study transforming a polar coordinate system
to a Cartesian system. This variation of area transformation
illustrates that the space as well as the perimeter is effected.
A projective transformation is
related to mapping, in which a three-dimensional form may be projected
onto a two-dimensional surface. In the vaulting of the CEBc a
far-reaching potential of projective geometry as a form generator
may be recognized. In the CEBc, the design process and the built
work can be enunciated geometrically. The buildings call upon
the spectator, not to dispassionately observe, but to emotionally
participate.
Order Nexus: Architecture and Mathematics
| abstract
index | Previous abstract | Next abstract | E-mail
John Clagett | Nexus Network Journal Homepage
|
 The Central
European Baroque church (CEBc) appears to be in endless conflict
with itself: at once unified and chaotic, continuous and fragmented.
Architects strived for Gesamtkunstwerk, architecture
and the plastic arts merging into a symphonic whole, and Zweischaligkeit,
in which contrasting tectonic systems coexist as a composite,
dissolving sharply-defined boundaries. The elements eternally
approach singularity: a dynamic continuum.
The Central
European Baroque church (CEBc) appears to be in endless conflict
with itself: at once unified and chaotic, continuous and fragmented.
Architects strived for Gesamtkunstwerk, architecture
and the plastic arts merging into a symphonic whole, and Zweischaligkeit,
in which contrasting tectonic systems coexist as a composite,
dissolving sharply-defined boundaries. The elements eternally
approach singularity: a dynamic continuum.