Lobachevskii Journal of Mathematics
Vol. 13, 2003, 45 – 50
©Niovi Kehayopulu and Michael Tsingelis
Niovi Kehayopulu and Michael Tsingelis
THE EMBEDDING OF AN ORDERED SEMIGROUP INTO AN
LE-SEMIGROUP
(submitted by M. M. Arslanov)
ABSTRACT. In this paper we prove the following: If
S is an ordered
semigroup, then the set P(S)
of all subsets of S with
the multiplication ” ∘ ”
on P(S) defined
by ”A ∘ B := (AB] if
A,B ∈P(S),
A≠∅,
B≠∅ and
A ∘ B := ∅ if
A = ∅ or
B = ∅
is an le-semigroup having a zero element and
S is embedded
in P(S).
|
________________
2000 Mathematical Subject Classification. 06F05.
|
If (S,.,≤) is an ordered
semigroup, for A ⊆ S,
we define (A] := {t ∈ S ∣ t ≤ a for some a ∈ A}.
For A = {a}, we write
(a] instead of
({a}]. An element 0
of S is called the
zero element of S
if 0 ≤ x and
0x = x0 = 0 for all
x ∈ S [1].
Let (S,.,≤),
(T,∘,≼) be ordered
semigroups, f : S → T a
mapping from S
into T.
The mapping f is
called isotone if x,y ∈ S,
x ≤ y implies
f(x) ≤ f(y).
f is called reverse
isotone if x,y ∈ S,
f(x) ≼ f(y) implies
x ≤ y. [Each reverse isotone
mapping is (1-1): Let x,y ∈ S,
f(x) = f(y). Since
f(x) ≼ f(y), we have
x ≤ y. Since
f(y) ≼ f(x), we
have y ≤ x.]
f
is called a homomorphism if it is isotone and satisfies
f(xy) = f(x) ∘ f(y) for all
x, y ∈ S.
f is
called an isomorphism if it is onto, homomorphism and reverse isotone.
S and
T
are called isomorphic if there exists an isomorphism between them [3].
S is embedded in
T if, by definition,
S is isomorphic to a
subset of T, i.e., if there
exists a mapping f : S → T
which is homomorphism and reverse isotone [4]. An l-semigroup (: lattice ordered semigroup)
is a semigroup S
at the same time a lattice satisfying the conditions
a(b ∨ c) = ab ∨ ac and
(a ∨ b)c = ac ∨ bc for all
a, b,c ∈ S [1].
By an le-semigroup we mean an l-semigroup having a greatest element
”e” (i.e.
e ≥ a for all
a ∈ S) [2]. We denote
by P(S) the set of
all subsets of S.
Theorem. Let (S,.,≤)
be an ordered semigroup. We define a multiplication
” ∘ ” on
P(S) as
follows:
∘ : P(S) ×P(S) →P(S) ∣ (A,B) → A ∘ B
where
A∘B : = (AB]ifA,B ∈P(S)∖{∅}
∅ ifA = ∅or B = ∅
Then (P(S),∘,⊆) is an le-semigroup
having a zero element and (S,.,≤)
is embedded in (P(S),∘,⊆).
Proof. First of all, the set P(S) in
non-empty. The multiplication ” ∘ ”
on P(S) is
well defined. Moreover, we have the following:
1) The multiplication ” ∘ ”
on P(S) is
associative. In fact:
Let A,B,C ∈P(S). If
A = ∅ or
B = ∅ or
C = ∅, then
(A ∘ B) ∘ C = ∅ and
A ∘ (B ∘ C) = ∅, so
(A ∘ B) ∘ C = A ∘ (B ∘ C).
Let A,B,C ∈P(S)∖{∅}. We
have A ∘ B,B ∘ C ∈P(S)∖{∅}.
Let now x ∈ (A ∘ B) ∘ C := ((A ∘ B)C].
Then x ≤ yc for
some y ∈ A ∘ B,
c ∈ C. Since
y ∈ A ∘ B := (AB], we have
y ≤ ab for
some a ∈ A,
b ∈ B.
Then
x ≤ (ab)c = a(bc); a ∈ A,bc ∈ BC ⊆ (BC] := B ∘ C,
so x ∈ (A(B ∘ C)] := A ∘ (B ∘ C).
Similarly, A ∘ (B ∘ C)] ⊆ (A ∘ B) ∘ C.
2) (P(S),∘,⊆) is
an le-semigroup:
Let A,B,C ∈P(S).
Then A ∘ (B ∪ C) = (A ∘ B) ∪ (A ∘ C).
Indeed:
If A = ∅,
then A ∘ (B ∪ C) = ∅,
A ∘ B = ∅,
A ∘ C = ∅.
If B = ∅,
then A ∘ (B ∪ C) = A ∘ C,
(A ∘ B) ∪ (A ∘ C) = A ∘ C.
If C = ∅,
then A ∘ (B ∪ C) = A ∘ B,
(A ∘ B) ∪ (A ∘ C) = A ∘ B.
Let A,B,C ∈P(S)∖{∅}.
We have
A ∘ (B ∪ C) := (A(B ∪ C)],A ∘ B := (AB],A ∘ C := (AC].
Since (AB], (AC] ⊆ (A(B ∪ C)],
we have (AB] ∪ (AC] ⊆ (A(B ∪ C)].
Let now t ∈ (A(B ∪ C)].
Then t ≤ ax for
some a ∈ A,
x ∈ B ∪ C. If
x ∈ B, then
t ∈ (AB] ⊆ (AB] ∪ (AC]. If
x ∈ C, then
t ∈ (AC] ⊆ (AB] ∪ (AC].
Similarly, for any A,B,C ∈P(S)∖{∅},
we have (A ∪ B) ∘ C = (A ∘ C) ∪ (B ∘ C).
Finally, S is the
greatest element and ∅
the zero element of P(S).
3) We consider the mapping
f : (S,.,≤) → (P(S),∘,⊆) ∣a → f(a) := (a].
The mapping f
is well defined. Moreover,
A) The mapping f
is a homomorphism. Indeed:
Let a,b ∈ S. We
have (a], (b] ∈P(S)∖{∅}
(since a ∈ (a],b ∈ (b]).
Thus we have
f(a) ∘ f(b) = (a] ∘ (b] := ((a](b]] = (ab] := f(ab).
Let a,b ∈ S,
a ≤ b. Then
f(a) := (a] ⊆ (b] := f(b).
B) The mapping f is
reverse isotone: Let a,b ∈ S,
f(a) ⊆ f(b).
Then
a ∈ (a] ⊆ (b], and
a ≤ b.
Remark. More generally, we have the following: If
A, Bi ∈P(S),
i ∈ I,
then
A ∘ (⋃
i∈IBi) = ⋃
i∈I(A ∘ Bi) and (⋃
i∈IBi) ∘ A = ⋃
i∈I(Bi ∘ A).
In fact,
A) If A = ∅,
then A ∘ (⋃
i∈I Bi) = ∅,
and A ∘ Bi = ∅ for
all i ∈ I, so
⋃
i∈I(A ∘ Bi) = ∅. Thus
A ∘ (⋃
i∈I Bi) = ⋃
i∈I(A ∘ Bi).
B) If A≠∅,
then
I) If ⋃
i∈I Bi = ∅,
then A ∘ (⋃
i∈I Bi) = ∅.
Since ⋃
i∈I Bi = ∅,
we have Bi = ∅
for all i ∈ I,
then A ∘ Bi = ∅ for
all i ∈ I,
and ⋃
i∈I(A ∘ Bi) = ∅.
Then
A ∘ (⋃
i∈I Bi) = ⋃
i∈I(A ∘ Bi).
II) Let ⋃
i∈I Bi≠∅.
We put J := {i ∈ I ∣ Bi = ∅},
K := {i ∈ I ∣ Bi≠∅}. Clearly
I = J ∪ K and
J ∩ K = ∅. If
K = ∅, then
I = J,
Bi = ∅ for all
i ∈ I, and
⋃
i∈IBi = ∅. Impossible.
Thus K≠∅.
α)
Let J = ∅.
Then I = K,
Bi ≠ ∅ for all
i ∈ I. Since
A≠∅ and
Bi ≠ ∅ for all
i ∈ I, we have
A ∘ Bi := (ABi] for all
i ∈ I. Then
⋃
i∈I(A ∘ Bi) = ⋃
i∈I(ABi].
Besides, ⋃
i∈I(ABi] = (A(⋃
i∈I Bi)].
Thus we have
⋃
i∈I(A ∘ Bi) = (A(⋃
i∈I Bi)]..........(∗)
Since A≠∅ and
(⋃
i∈I Bi)≠∅, we have
A ∘ (⋃
i∈I Bi) = (A(⋃
i∈I Bi)]. Then, by
(*), A ∘ (⋃
i∈I Bi) = ⋃
i∈I(A ∘ Bi).
β)
Let J≠∅.
Then Bi = ∅ for
all i ∈ I,
⋃
i∈IBi = ∅,
and
∅≠⋃
i∈I Bi = (⋃
i∈J Bi) ∪ (⋃
i∈K Bi) = ⋃
i∈K Bi.
Since A≠∅
and ⋃
i∈I Bi≠∅,
we have
A ∘ (⋃
i∈I Bi) = (A(⋃
i∈I Bi)] = (A(⋃
i∈K Bi)] = ⋃
i∈K(ABi].
Since A≠∅
and Bi≠∅ for
all i ∈ K, we
have A ∘ Bi := (ABi] for
all i ∈ K,
and ⋃
i∈K(A ∘ Bi) = ⋃
i∈K(ABi].
Thus we have
A ∘ (⋃
i∈I Bi) = ⋃
i∈K(A ∘ Bi)..........(∗∗)
Since Bi = ∅
for all i ∈ J,
we have A ∘ Bi = ∅
for all i ∈ J,
then ⋃
i∈J(A ∘ Bi) = ∅.
Then
⋃
i∈K(A ∘ Bi) ∪⋃
i∈J(A ∘ Bi) = ⋃
i∈K(A ∘ Bi)..........(∗∗∗)
By (**) and (***), we have
A ∘ (⋃
i∈I Bi) = ⋃
i∈K(A ∘ Bi) ∪⋃
i∈J(A ∘ Bi) = ⋃
i∈K∪J(A ∘ Bi) = ⋃
i∈J(A ∘ Bi).□
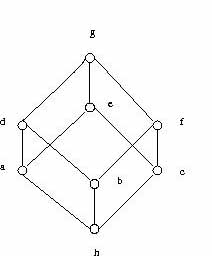
Example. We consider the ordered semigroup
S = {x,y,z}
defined by the multiplication and the figure below:
Applying the Theorem of this note, the ordered semigroup
(S,.,≤) is embedded into the
le-semigroup L = {a,b,c,d,e,f,g,h}, defined by
the multiplication ”.”and
the order ” ≤L”
below:
| . | a | b | c | d | e | f | g | h |
|
|
|
|
|
|
|
|
|
| a | a | a | g | a | g | g | g | h |
|
|
|
|
|
|
|
|
|
| b | a | b | g | d | g | g | g | h |
|
|
|
|
|
|
|
|
|
| c | a | g | g | g | g | g | g | h |
|
|
|
|
|
|
|
|
|
| d | a | d | g | d | g | g | g | h |
|
|
|
|
|
|
|
|
|
| e | a | g | g | g | g | g | g | h |
|
|
|
|
|
|
|
|
|
| f | a | g | g | g | g | g | g | h |
|
|
|
|
|
|
|
|
|
| q | a | g | g | g | g | g | g | h |
|
|
|
|
|
|
|
|
|
| h | h | h | h | h | h | h | h | h |
≤L :={(a,a), (a,d), (a,e), (a,g), (b,b), (b,d), (b,f), (b,g), (c,d), (c,e),
(c,f), (c,g), (d,d), (d,g), (e,e), (e,g), (f,f), (f,g), (g,g), (h,a),
(h,b), (h,c), (h,d), (h,e), (h,f), (h,g), (h,h)}.
We give the covering relation ”≺’
and the figure of S.
≺={(a,d), (a,e), (b,d), (b,f), (c,e), (c,f), (d,g), (e,g), (f,g),
(h,a), (h,b), (h,c)}.
The embedding is given by the mapping:
f : (S,.,≤) → (L,.,≤L) x → a
y → b
z → g
This research was supported by the Special Research Account of the University of
Athens (Grant No. 5630).
References
[1] Birkhoff G., ”Lattice Theory”, Amer. Math. Soc. Coll. Publ. Vol. XXV, Providence,
Rh. Island, 1967.
[2] Kehayopulu N., On intra-regular ∨e-semigroups,
Semigroup Forum 19 (1980), 111-121.
[3] Kehayopulu N. and M. Tsingelis, On subdirectly irreducible ordered semigroups,
Semigroup Forum 50 (1995), 161-177.
[4] Kehayopulu N. and M. Tsingelis, The embedding of an ordered
semigroup in a simple one with identity, Semigroup Forum 53 (1996), 346-350.
UNIV. OF ATHENS, DEPT. OF MATHEMATICS;
HOME ADDRESS: NIOVI KEHAYOPULU, NIKOMIDIAS 18, 161 22 KESARIANI,
GREECE
E-mail address: nkehayop@cc.uoa.gr
Received September 30, 2003