We study a particular number pyramid
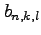
that relates the
binomial,
Deleham, Eulerian, MacMahon-type and Stirling number triangles. The
numbers
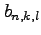
are generated by a function
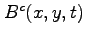
,
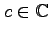
, that
appears in the calculation of derivatives of a class of functions whose
derivatives can be expressed as polynomials in the function itself or a related function. Based on
the properties of the numbers
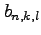
, we derive several new relations related to these triangles.
In particular, we show that the
number triangle
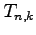
, recently constructed by Deleham (Sloane's
A088874) and
is generated by the Maclaurin series of
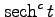
,
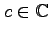
.
We also give explicit expressions and various partial sums for
the triangle
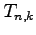
. Further, we find that
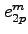
, the
numbers appearing in the Maclaurin series of
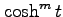
, for all
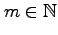
, equal the number of closed walks, based at a vertex, of length
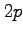
along the edges of an
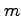
-dimensional cube.

