Let
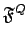
be the set of Farey fractions of order
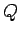
.
Given the integers
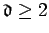
and
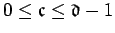
, let
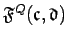
be
the subset of
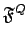
of those fractions whose denominators are
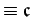
(mod
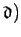
, arranged in ascending order. The problem we
address here is to show that as
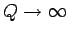
,
there exists a limit probability measuring the distribution of
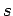
-tuples
of consecutive denominators of fractions in
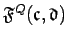
.
This shows that the clusters of points
![$ (q_0/Q,q_1/Q,\dots,q_s/Q)\in[0,1]^{s+1}$](abs/img10.gif)
, where
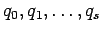
are consecutive denominators of members of
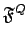
produce a limit set,
denoted by
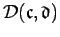
.
The shape and the structure of this set are presented in several
particular cases.
Received September 15 2004;
revised version received May 20 2005; July 20 2006.
Published in Journal of Integer Sequences July 20 2006.

