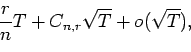We analyze the asymptotic behavior of the average maximal number of balls in a bin obtained by throwing uniformly at random r balls without replacement into n bins, T times. Writing the expected maximum as

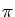
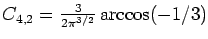
a recent preprint of Behrouzi-Far and Zeilberger asks for an explicit expression for C_n,r in terms of n,r and . In this short note, we find an expression for C_n,r in terms of n, r and the expected maximum of n independent standard Gaussians. This provides asymptotics for large n as well as closed forms for small n--e.g., --and shows that computing a closed form for C_n,r is precisely as hard as the difficult question of finding the expected maximum of n independent standard Gaussians.