Some Double Sums Involving Ratios of Binomial Coefficients Arising From Urn Models

Some Double Sums Involving Ratios of Binomial Coefficients Arising From Urn Models

David Stenlund
Mathematics and Statistics
Åbo Akademi University
FI-20500 Åbo
Finland

James G. Wan
Engineering Systems and Design
Singapore University of Technology and Design
8 Somapah Road, 487372
Singapore
and
School of Mathematical and Physical Sciences
The University of Newcastle
University Drive
Callaghan NSW 2308
Australia

Abstract:

In this paper we discuss a class of double sums involving ratios of binomial coefficients. The sums are of the form

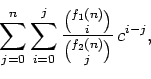
$\begin{displaymath}\sum_{j=0}^{n} \sum_{i=0}^j \frac{\binom{f_1(n)}{i}}{\binom{f_2(n)}{j}}\,c^{i-j}, \end{displaymath}$

where f₁, f₂ are functions of n. Such sums appear in the analyses of the Mabinogion urn and the Ehrenfest urn in probability. Using hypergeometric functions, we are able to simplify these sums, and in some cases express them in terms of the harmonic numbers.

Full version: pdf, dvi, ps, latex

Received September 25 2018; revised version received January 24 2019. Published in Journal of Integer Sequences, February 15 2019.

Return to Journal of Integer Sequences home page