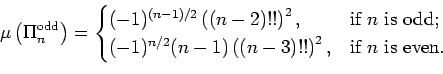The Möbius number of a finite poset is a very useful combinatorial invariant of the poset that generalizes the classical number-theoretic Möbius function. The Möbius number of the poset of partitions
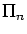
of a set with
n elements is well-known. A related poset, the subposet consisting only of partitions that use odd part size or the maximum element
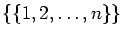
,
written
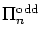
,
arises in similar combinatorial settings. In this paper, we compute the Möbius numbers of all
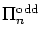
as follows:
This result was first stated as known by Stanley and has since been proven by Sundaram and Wachs. They constructed versions of the formula above by respectively using symmetric function/representation theory and topological/simplicial complex techniques. In this paper, we provide a new proof using only elementary combinatorial techniques and the WZ algorithm.