 |
Journal of Integer Sequences, Vol. 20 (2017), Article 17.7.1 |
 |
Journal of Integer Sequences, Vol. 20 (2017), Article 17.7.1 |
Abstract:
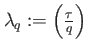 where
where
(Concerned with sequences
A000005
A008836
A091337.)
Received January 14 2017; revised versions received June 1 2017; June 26 2017. Published in Journal of Integer Sequences, July 1 2017.