Journal of Integer Sequences, Vol. 17 (2014), Article 14.8.6

On the Powerful and Squarefree Parts of an Integer


Maurice-Étienne Cloutier, Jean-Marie De Koninck, and Nicolas Doyon
Département de mathématiques et de statistique
Université Laval
Québec G1V 0A6
Canada

Abstract:

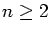
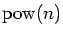
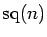
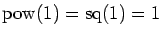
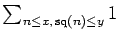
Any integer $n\ge 2$ can be written in a unique way as the product of its powerful part and its squarefree part, that is, as n=mr where m is a powerful number and r a squarefree number, with gcd(m,r)=1. We denote these two parts of an integer n by $\pow(n)$ and $\sq(n)$respectively, setting for convenience $\pow(1)=\sq(1)=1$. 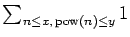We first examine the behavior of the counting functions $\sum_{n\le x,\, {\scriptsize\sq}(n)\le y} 1$ and $\sum_{n\le x,\, {\scriptsize \pow}(n)\le y} 1$. 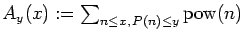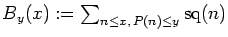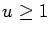Letting P(n) stand for the largest prime factor of n, we then provide asymptotic values of $A_y(x):=\sum_{n\le x,\, P(n)\le y} \pow(n)$ and $B_y(x) :=\sum_{n\le x,\, P(n)\le y} \sq(n)$when y=x1/u with $u\ge 1$ fixed. 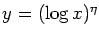We also examine the size of Ay(x) and By(x) when $y=(\log x)^\eta$ for some $\eta1$. 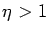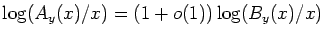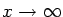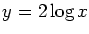Finally, we prove that Ay(x) will coincide with By(x) in the sense that $\log(A_y(x)/x) = (1+o(1))\log(B_y(x)/x)$ as $x\to \infty$ if we choose $y=2\log x$.

Full version:  pdf,    dvi,    ps,    latex    

Received July 8 2014; revised version received July 31 2014. Published in Journal of Integer Sequences, August 5 2014.

Return to Journal of Integer Sequences home page