 |
Journal of Integer Sequences, Vol. 16 (2013), Article 13.7.8 |
 |
Journal of Integer Sequences, Vol. 16 (2013), Article 13.7.8 |
Abstract:
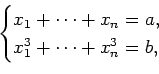
Received August 4 2013; revised version received September 4 2013. Published in Journal of Integer Sequences, September 8 2013. Minor revision, November 1 2013.