Journal of Integer Sequences, Vol. 16 (2013), Article 13.7.6

Note on the Convolution of Binomial Coefficients


Rui Duarte
Center for Research and Development in Mathematics and Applications
Department of Mathematics
University of Aveiro
Portugal

António Guedes de Oliveira
CMUP and Department of Mathematics
Faculty of Sciences
University of Porto
Portugal

Abstract:

We prove that, for every integer a, real numbers k and $\ell$, and nonnegative integers n, i and j,

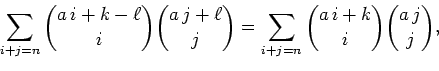
\begin{displaymath}\sum_{i+j=n} {a\,i+k-\ell\choose i} {a\,j+\ell\choose j} = \sum_{i+j=n} {a\,i+k\choose i} {a\,j\choose j}, \end{displaymath}

by presenting explicit expressions for its value. We use the identity to generalize a recent result of Chang and Xu, and end the paper by presenting, in explicit form, the ordinary generating function of the sequence $\left\{{2n+k\choose n}\right\}_{n=0}^\infty$, where $k\in \mathbb{R} $.

Full version:  pdf,    dvi,    ps,    latex    

(Concerned with sequences A000302 A000984 A006256 A078995.)

Received February 8 2013; revised versions received March 8 2013; July 26 2013; August 21 2013. Published in Journal of Integer Sequences, August 22 2013.

Return to Journal of Integer Sequences home page