We develop techniques that can be applied to find solutions to the
recurrence
![$ \genfrac{\vert}{\vert}{0pt}{}{n}{k} = (\alpha n + \beta k + \gamma) \genfrac{\...
...lpha' n + \beta' k + \gamma') \genfrac{\vert}{\vert}{0pt}{}{n-1}{k-1} + [n=k=0]$](abs/img2.gif)
. Many
interesting combinatorial numbers, such as binomial coefficients, both
kinds of Stirling and associated Stirling numbers, Lah numbers,
Eulerian numbers, and second-order Eulerian numbers, satisfy special
cases of this recurrence. Our techniques yield explicit expressions in
the instances
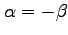
,
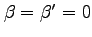
, and
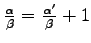
, adding to the result
of Neuwirth on the case
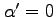
. Our approach employs finite
differences, continuing work of the author on using finite differences
to study combinatorial numbers satisfying simple recurrences. We also
find expressions for the power sum
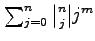
for
some special cases of the recurrence, and we prove some apparently new
identities involving Stirling numbers of the second kind, Bell numbers,
Rao-Uppuluri-Carpenter numbers, second-order Eulerian numbers, and both
kinds of associated Stirling numbers.
Received October 18 2010;
revised version received October 19 2011.
Published in Journal of Integer Sequences, November 21 2011.

