Journal of Integer Sequences, Vol. 13 (2010), Article 10.1.5

Divisibility by 3 of Even Multiperfect Numbers of Abundancy 3 and 4


Kevin A. Broughan and Qizhi Zhou
University of Waikato
Hamilton, New Zealand

Abstract:

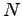
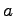
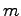
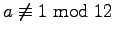
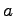
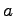
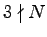
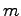
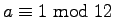
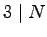
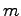
We say a number is flat if it can be written as a non-trivial power of 2 times an odd squarefree number. The power is the ``exponent" and the number of odd primes the ``length". Let $N$ be flat and 4-perfect with exponent $a$ and length $m$. If $a\not\equiv 1\bmod 12$, then $a$ is even. If $a$ is even and $3\nmid N$ then $m$ is also even. If $a\equiv 1\bmod 12$ then $3\mid N$ and $m$ is even. 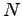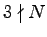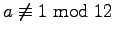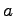If $N$ is flat and 3-perfect and $3\nmid N$, then if $a\not\equiv 1\bmod 12$, $a$ is even. 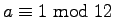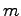If $a\equiv 1\bmod 12$ then $m$ is odd. 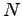If $N$ is flat and 3 or 4-perfect then it is divisible by at least one Mersenne prime, but not all odd prime divisors are Mersenne. We also give some conditions for the divisibility by 3 of an arbitrary even 4-perfect number.

Full version:  pdf,    dvi,    ps,    latex    

(Concerned with sequences A005820 and A027687.)

Received June 30 2009; revised versions received October 12 2009; January 7 2010. Published in Journal of Integer Sequences, January 8 2010.

Return to Journal of Integer Sequences home page