A prime number
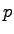
is called
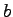 -elite
-elite if only finitely many generalized Fermat
numbers
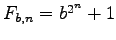
are quadratic residues modulo
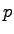
. Let
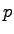
be a prime. Write
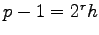
with
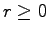
and
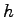
odd. Define the length of the
b-Fermat period of 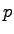
to be the minimal natural
number
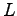
such that
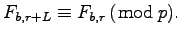
Recently Müller and Reinhart derived three
conjectures on
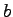 -elite
-elite primes, two of them being the following. (1) For every natural number
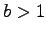
there
is a
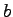 -elite
-elite prime. (2) There are generalized elite primes with elite periods of arbitrarily large lengths. We
extend Müller and Reinhart's observations and computational results to further support above two conjectures. We
show that Conjecture 1 is true for
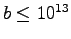
and that for every possible length
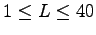
there actually exists a generalized elite prime with elite period length
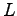
.

