For any integer
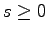
, we derive a combinatorial interpretation
for the family of sequences generated by the recursion
(parameterized by
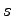
)
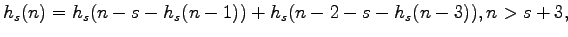
with the
initial conditions
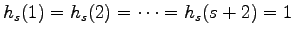
and
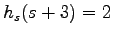
. We show how these sequences count the number of
leaves of a certain infinite tree structure. Using this
interpretation we prove that
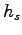
sequences are ``slowly
growing'', that is,
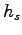
sequences are monotone nondecreasing,
with successive terms increasing by 0 or 1, so each sequence hits
every positive integer. Further, for fixed
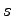
the sequence
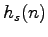
hits every positive integer twice except for powers of 2, all of
which are hit
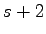
times. Our combinatorial interpretation provides
a simple approach for deriving the ordinary generating functions for
these sequences.

