|
ACTA
MATHEMATICA
|
On solutions of a system of rational difference equations
Yu Yang, Li Chen and Yong-Guo Shi
Received: February 10, 2009; Accepted: September 25, 2010
Abstract. In this paper we investigate the system of rational difference equations
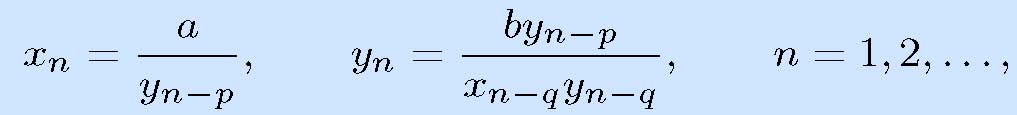
where q is a positive integer with p q, p \not | q, p is an odd number and p ³ 3, both a and b are nonzero real constants and the initial values x-q+1, x-q+2, . . . x0, y-q+1, y-q+2, . . ., y0 are nonzero real numbers. We show all real solutions of the system are eventually periodic with period 2pq (resp. 4pq) when (a/b)q = 1 (resp. (a/b)q = -1), characterize the asymptotic behavior of the solutions when a ³ b, which generalizes Őzban's results of in [Appl. Math. Comput. 188 (2007), 833-837].
Keywords: System of difference equations; homogeneous equations of degree one; eventually periodic solutions.
AMS Subject classification: Primary: 39A11, 37B20.
PDF Compressed Postscript Version to read
ISSN 0862-9544 (Printed edition)
Faculty of Mathematics, Physics and Informatics
Comenius University
842 48 Bratislava, Slovak Republic
Telephone: + 421-2-60295111 Fax: + 421-2-65425882
e-Mail: amuc@fmph.uniba.sk Internet: www.iam.fmph.uniba.sk/amuc
© 2011, ACTA MATHEMATICA UNIVERSITATIS COMENIANAE