|
ACTA
MATHEMATICA
|
p. 137 - 144
Strong stably finite rings and some extensions
M. R. Vedadi
Received: March 16, 2008; Revised: September 17, 2008; Accepted: September 22, 2008
Abstract. A ring R is called right strong stably finite (r.ssf) if for all n > 1, injective endomorphisms of RnR are essential. If R is an r.ssf ring and eR is an idempotent of R such that eR is a retractable R-module, then eRe is an r.ssf ring. A direct product of rings is an r.ssf ring if and only if each factor is so. R.ssf condition is investigated for formal triangular matrix rings. In particular, if M is a finitely generated module over a commutative ring R such that for all n > 1, M(n)R is co-Hopfian, then
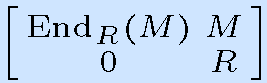is an r.ssf ring. If X is a right denominator set of
regular elements of R, then R
is an r.ssf ring if and only if RX –1 is so.
Keywords: Co-Hopfian; Ore ring; strong stably finite; weakly co-Hopfian.
AMS Subject classification: Primary: 16D10, 16D90 Secondary: 16P40, 16S10
PDF Compressed Postscript Version to read
ISSN 0862-9544 (Printed edition)
Faculty of Mathematics, Physics and Informatics
Comenius University
842 48 Bratislava, Slovak Republic
Telephone: + 421-2-60295111 Fax: + 421-2-65425882
e-Mail: amuc@fmph.uniba.sk Internet: www.iam.fmph.uniba.sk/amuc
© 2009, ACTA MATHEMATICA UNIVERSITATIS COMENIANAE